Бинарные отношения. Основные определения
Двухместным, или бинарным, отношением R называется подмножество пар (а, b)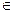 R прямого произведения М1 × М2, т.е. R
R прямого произведения М1 × М2, т.е. R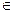 М1 × М2. При этом множество М1 называют областью определения отношения R, множество М2 - областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М, тогда R
М1 × М2. При этом множество М1 называют областью определения отношения R, множество М2 - областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М, тогда R М х М. Если a, b находятся в отношении R, это часто записывается как аRb.
М х М. Если a, b находятся в отношении R, это часто записывается как аRb.
Пусть R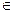 А х В определено в соответствии с изображением на рисунке 2.1. Область определения D(R) и область значений Q(R) определяются соответственно:
А х В определено в соответствии с изображением на рисунке 2.1. Область определения D(R) и область значений Q(R) определяются соответственно:
D(R) = {a: (a, b)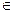 R},
R},
Q(R) = {b: (a, b)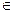 R}.
R}.

Рисунок 2.1
Способы задания бинарных отношений - любые способы задания множеств (так как отношения определены выше как подмножества некоторых множеств - прямых произведений). Отношения, определенные на конечных множествах, обычно задаются:
1. Списком (перечислением) пар, для которых это отношение выполняется. Например, R = {(а, b), (а, с), (b,d)}.
2. Матрицей - бинарному отношению R М х М, где М= {аг а2,..., ап}, соответствует квадратная матрица порядка п, в которой элемент сij.., стоящий на пересечении i-и строки j-го столбца, равен 1, если между аi и aj имеет место отношение R или 0, если оно отсутствует:
М х М, где М= {аг а2,..., ап}, соответствует квадратная матрица порядка п, в которой элемент сij.., стоящий на пересечении i-и строки j-го столбца, равен 1, если между аi и aj имеет место отношение R или 0, если оно отсутствует:

Пример 1.Пусть М= {1,2,3,4,5,6}. Задать в явном виде (списком) и матрицей отношение R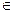 М× М, если R означает - "быть строго меньше".
М× М, если R означает - "быть строго меньше".
Отношение R как множество содержит все пары элементов а, b из М такие, что а < b:
R = {(а, b): а,b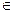 М;а< b}.
М;а< b}.
Тогда R = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}.
Матрица отношения приведена на рисунке 2.2.
| R | ||||||
Рисунок 2.2
Пример 2.Пусть М= {1,2,3,4,5,6}. Составить матрици отношения R1, R2, R3  M×М, если:
M×М, если:
1) R1 – “быть делителем”;
2) R2 – “иметь общий делитель”;
3) R3 –“иметь один и тот же остаток от деления на 3”.
1. R1={(a, b): a,b 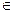 M; a – делитель b} и выполняется для пар {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)}. Эти пары (a,b)
M; a – делитель b} и выполняется для пар {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)}. Эти пары (a,b)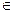 R1 определяют наличие единицы в матрице отношения R1
R1 определяют наличие единицы в матрице отношения R1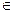 M2 на пересечении строки элемента а и столбца b, а,b
M2 на пересечении строки элемента а и столбца b, а,b 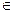 М (рисунок 2.3).
М (рисунок 2.3).
| R | ||||||
Рисунок 2.3
2. R2={(a, b): a,b 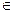 M; a и b имеют общий делитель, с
M; a и b имеют общий делитель, с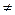 1}. Матрица отношения приведена на рисунке 2.4.
1}. Матрица отношения приведена на рисунке 2.4.
| R | ||||||
Рисунок 2.4
3. R3={(a, b): a,b 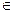 M; a и b имеют один и тот же остаток от деления на 3}. Матрица отношения приведена на рисунке 2.5.
M; a и b имеют один и тот же остаток от деления на 3}. Матрица отношения приведена на рисунке 2.5.
| R | ||||||
Рисунок 2.5
1.2.2. Свойства бинарных отношений
Пусть R - отношение на множестве М, R М х М. Тогда:
М х М. Тогда:
1) R -рефлексивно, если имеет место a R а для любого а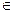 М (например, отношение "жить в одном городе" - рефлексивно);
М (например, отношение "жить в одном городе" - рефлексивно);
2) R - антирефлексивно, если ни для какого а 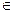 М не выполняется a R а (например, отношение "быть сыном" - антирефлексивно);
М не выполняется a R а (например, отношение "быть сыном" - антирефлексивно);
3) R - симметрично, если a R b влечет b R а (например, отношение "работать на одной фирме" - симметрично);
4) R - антисимметрично, если a R b и b R а влекут а = b, т.е. ни для каких различающихся элементов а и b (а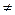 b) не выполняется одновременно aRb и bRа (например, отношения "быть сыном", "быть начальником" - антисимметричны);
b) не выполняется одновременно aRb и bRа (например, отношения "быть сыном", "быть начальником" - антисимметричны);
5) R - транзитивно, если aRb и bRc влекут aRс (например, отношения "быть моложе", "быть братом" - транзитивны).