Декартовых координатах

Вычисление двойного интеграла в прямоугольных

Пусть требуется вычислить двойной интеграл , где область — прямоугольник, определяемый неравенствами , .

Предположим, что 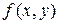непрерывна в этом прямоугольнике и принимает в нем неотрицательные значения, тогда данный двойной интеграл равен объему тела с основанием , ограниченного сверху поверхностью , с боков — плоскостями , , , :

С другой стороны, объем такой фигуры можно вычислить с помощью определенного интеграла:

где — площадь сечения данного тела плоскостью, проходящей через точку и перпендикулярной к оси . А так как рассматриваемое сечение является криволинейной трапецией , ограниченной сверху графиком функции , где фиксировано, а , то

Из этих трех равенств следует, что

Итак, вычисление данного двойного интеграла свелось к вычислению двух определенных интегралов; при вычислении «внутреннего интеграла» (записанного в скобках) считается постоянным.

Замечание. Можно доказать, что последняя формула верна и при , а также в случае, когда функция 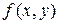меняет знак в указанном прямоугольнике.

Правая часть формулы называется повторным интегралом и обозначается так:

Аналогично можно показать, что

Из выше сказанного следует, что

Последнее равенство означает, что результат интегрирования не зависит от порядка интегрирования.

Чтобы рассмотреть более общий случай, введем понятие стандартной области. Стандартной ( или правильной ) областью в направлении данной оси называется такая область, для которой любая прямая, параллельная этой оси пересекает границу области не более, чем в двух точках. Другими словами, пересекает саму область и ее границу только по одному отрезку прямой.

Предположим, что ограниченная область является стандартной в направлении оси и ограничена сверху графиком функции , снизу — графиком функции . Пусть R{, } — минимальный прямоугольник, в котором заключена данная область .

Пусть в области определена и непрерывна функция . Введем новую функцию:

тогда в соответствии со свойствами двойного интеграла

И, следовательно,

Поскольку отрезок целиком принадлежит области то, следовательно, при , а если лежит вне этого отрезка, то .

При фиксированном можем записать:

Так как первый и третий интегралы в правой части равны нулю, то

Следовательно,

Из чего получаем формулу для вычисления двойного интеграла по области, стандартной относительно оси путем сведения к повторному интегралу:

Если область является стандартной в направлении оси и определяется неравенствами , , аналогично можно доказать, что

Замечание. Для области , стандартной в направлении осей и , будут выполнены оба последних равенства, поэтому

По этой формуле осуществляется изменение порядка интегрирования при вычислении соответствующего двойного интеграла.

Замечание. Если область интегрирования не является стандартной (правильной) в направлении обеих осей координат, то ее разбивают на сумму стандартных областей и представляют интеграл в виде суммы интегралов по этим областям.

Пример. Вычислить двойной интегралпо области , ограниченной линиями: , , .

Решение. Изобразим на рисунке заданную область интегрирования.

Данная область является стандартной как относительно оси , так и относительно оси .

Вычислим интеграл, считая область стандартной относительно оси .