Полный дифференциал функции нескольких переменных
.
Выясним, как переносятся условия дифференцируемости на случай функции двух переменных.
Определение.Функция 
называется дифференцируемой в точке 
, если ее полное приращение в этой точке можно представить в виде
, (1)
где 
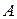и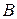 
— некоторые постоянные, зависящие от 
и 
; 
и 
— функции от 
и 
, стремящиеся к нулю при 
и 
, то есть 
, 
.
Равенство (1) выражает условие дифференцируемости функции в точке .
Определение.Функцию , дифференцируемую в каждой точке некоторого множества, называют дифференцируемой на этом множестве.
Например, функция 
дифференцируема на всей плоскости 
. Действительно, полное приращение данной функции в любой точке 
R2 имеет вид
Положив 
, 
, 
, 
, получим представление 
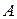в виде (1), так как и 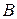в фиксированной точке будут постоянными, а
, .
Условие дифференцируемости функции в точке можно записать в виде:
, (2)
где 
— расстояние между точками и 
:
.
При этом 
.
Очевидно, что если и , то и 
, и наоборот, если , то и , а следовательно, и стремятся к нулю. Тогда в равенстве (1) сумму 
можно переписать в виде
,
так как 
, 
и 
.
Справедливо и обратное утверждение: из представимости в форме (2) следует равенство (1), т. е. условия дифференцируемости (1) и (2) функции в точке эквивалентны.
В равенствах (1) и (2) слагаемое 
, линейное относительно и 
, называют главной частью приращения функции, так как оставшееся слагаемое 
является бесконечно малой функцией более высокого порядка малости, чем , при и .
Установим теперь связь между дифференцируемостью и непрерывностью функции двух переменных.
Теорема.Если функция дифференцируема в точке ,то она и непрерывна в этой точке.
Доказательство. Действительно, по определению функции, дифференцируемой в точке , ее приращение представимо в виде
,
где , 
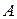, и 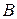— некоторые числа, не зависящие от и .
Следовательно,
,
а это означает, что функция непрерывна в точке .
Теорема доказана.
Теорема (необходимое условие дифференцируемости функции).Если функция дифференцируема в точке , то она имеет в этой точке частные производные 
и 
, причем 
, 
.
Доказательство. Пусть функция дифференцируема в точке ,тогда ее приращение представимо в виде (1). Положив в формуле (1) 
,имеем 
. Разделив это равенство на и перейдя к пределу при , получим
.
Следовательно, в точке существует частная производная 
.
Аналогично доказывается существование частной производной 
в точке
Теорема доказана.
Утверждения, обратные утверждениям данных теорем , неверны, т. е. из непрерывности функции, а также существования ее частных производных, еще не следует дифференцируемость функции.
Например, функция 
непрерывна в точке О(0; 0), но не имеет в этой точке частных производных. Действительно,
.
Функция 
не имеет предела при . Следовательно, 
(0; 0) не существует.
Аналогично доказывается, что не существует 
(0; 0).
Для того, чтобы функция была дифференцируема в точке , на нее налагают условия более жесткие, чем существование частных производных.
Теорема (достаточное условие дифференцируемости функции).Если функция имеет частные производные в некоторой окрестности точки , непрерывные в самой этой точке, то она дифференцируема в точке , причем формулу (1) можно представить в виде:
.
Определение.Функции с непрерывными частными производными называются непрерывно дифференцируемыми.
Например, функция 
дифференцируема в любой точке 
R2 так как ее частные производные 
и 
всюду непрерывны.
Напомним, что для функции одной переменной существование производной в точке является необходимым и достаточным условием ее дифференцируемости в этой точке.
Понятие дифференцируемости для функции трех и более переменных вводится аналогично. Дадим, например, определение дифференцируемости функции трех переменных. Функция 
,определенная в 
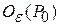,называется дифференцируемой в точке 
,если ее полное приращение представимо в виде
,
где 
, 
и 
— некоторые постоянные, зависящие от , и 
; , и 
—бесконечно малые функции при , и 
.
Определение. Функция любого числа переменных, дифференцируемая в каждой точке некоторого множества, называется дифференцируемой на этом множестве.
Если функция дифференцируема в точке , то, как было показано выше, ее полное приращение в этой точке можно представить в виде
.
Сумма первых двух слагаемых есть главная линейная (относительно и ) часть приращения функции.
Определение. Если функция дифференцируема в точке , то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается
.
Приращения независимых переменных и называют дифференциалами независимых переменных 
и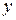 
и обозначают соответственно 
и 
. Тогда полный дифференциал функции можно записать в виде:
или в более краткой форме: 
.
Пример. Найти полный дифференциал функции 
.
Решение. 
для 
.
Пример. Найти полный дифференциал функции 
.
Решение. Найдем частные производные функции:
,
.
Следовательно,
для .
Определение полного дифференциала легко обобщается на случай функции любого числа переменных. Например, полным дифференциалом функции трех переменных в точке 
называется главная, линейная относительно приращений всех аргументов, часть полного приращения функции, т. е.
.
Из определения дифференциала функции нескольких переменных следует, что для функции можно полагать 
, а для функции , зависящей от трех переменных 
, для 
,
.
Эти соотношения позволяют получить формулы для приближенного вычисления значений функции:
,
.
И в общем случае,
.
Полный дифференциал чаще используется для оценки погрешности вычислений по формулам.
Например, если задана дифференцируемая функция 
переменных 
. Тогда абсолютная погрешность 
вычислений по этой формуле оценивается величиной
,
а относительная погрешность ― величиной 
.