Поверхности (линии) уровня
Пусть в трехмерном пространстве имеется область D, в которой задана функция
 .
.
В этом случае говорят, что в области D задано скалярное поле.
Если, например, функция  обозначает температуру в точке
обозначает температуру в точке  , то говорят, что задано скалярное поле температур; если область D заполнена жидкостью или газом и
, то говорят, что задано скалярное поле температур; если область D заполнена жидкостью или газом и  обозначает давление, то имеется скалярное поле давлений и т. д.
обозначает давление, то имеется скалярное поле давлений и т. д.
Рассмотрим точки области D, в которых функция  имеет постоянное значение
имеет постоянное значение  :
:
 .
.
Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение  , то получим другую поверхность. Эти поверхности называются поверхностями уровня.
, то получим другую поверхность. Эти поверхности называются поверхностями уровня.
Пример. Пусть задано скалярное поле
 .
.
Здесь поверхностями уровня будут поверхности
 ,
,
т. е. эллипсоиды с полуосями  ,
,  ,
,  .
.
Если функция 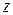 есть функция двух переменных
есть функция двух переменных  и
и 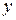 :
:
 ,
,
то «поверхностями» уровня будут линии на плоскости  :
:
 ,
,
которые называются линиями уровня.
Если значения 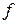 мы будем откладывать по оси
мы будем откладывать по оси  , то линиями уровня на плоскости
, то линиями уровня на плоскости  будут проекции линий, которые получаются в пересечении поверхности
будут проекции линий, которые получаются в пересечении поверхности  с плоскостями
с плоскостями  . Зная линии уровня, легко исследовать характер поверхности
. Зная линии уровня, легко исследовать характер поверхности  .
.

Пример.Определить линии уровня функции  .
.
Решение. Линиями уровня будут линии с уравнениями  . Это окружности радиуса
. Это окружности радиуса  . В частности, при
. В частности, при  получаем окружность
получаем окружность  . График данной функции, а также получаемые линии уровня изображены на рисунке.
. График данной функции, а также получаемые линии уровня изображены на рисунке.
