Понятие функции нескольких переменных

Криволинейные интегралы второго рода

Кратные интегралы

Функции нескольких переменных

СОДЕРЖАНИЕ

Понятие функции нескольких переменных………………………….……..5

Поверхности (линии) уровня……………………………….…………...…...8

Предел функции нескольких переменных…………………………….……10

Непрерывность функций нескольких переменных…………………….….12

Дифференцирование функций нескольких переменных……………….…13

Дифференцируемость функций нескольких переменных………………...17

Необходимое и достаточное условия дифференцируемости

Полный дифференциал функции нескольких переменных……..……..….21

Дифференцирование сложной функции……………………..……….….…23

Дифференцирование функции, заданной неявно……………………...…..25

Частные производные и дифференциалы высших порядков……………..27

Локальные экстремумы функции двух переменных……………………….30

Касательная плоскость и нормаль к поверхности………………………..…35

Производная по направлению………………………………………………..37

Градиент функции………………………………….…………………….…...39

 

Задачи, приводящие к двойным интегралам. Определение

двойного интеграла………………………………………………..……..…..41

Свойства двойного интеграла……………………………………………..…44

Вычисление двойного интеграла в прямоугольных

декартовых координатах……………………………………..………………45

Вычисление двойного интеграла в полярной системе координат…..…….52

Тройной интеграл…………………………………………………….………55

 

Задача о вычислении работы переменной силы.

Определение криволинейного интеграла второго рода…………….……..59

Криволинейный интеграл второго рода в координатной форме….………61

Вычисление криволинейных интегралов второго рода…………….…..…62

Формула Грина……………………………………………………….………67

Условия независимости криволинейного интеграла

от пути интегрирования…………………...………………………….……..70

Литература……………………………………………………………..……..73

При изучении многих явлений приходится встречаться с функциями двух и более независимых переменных. Приведем несколько примеров.

 

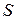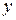Пример. Площадь прямоугольника со сторонами, длины которых равны и , выражается формулой

.

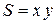Каждой паре значений и 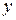соответствует определенное значение площади 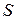. 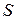есть функция двух переменных.

 

Пример. Объем 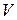прямоугольного параллелепипеда с ребрами, длины которых равны ,,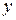, 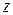выражается формулой

.

Здесь 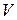есть функция трех переменных ,,.

 

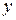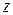Пример.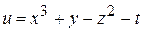

Здесь есть функция четырех переменных , , , .

 

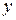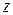Определение.Множество всех упорядоченных наборов действительных чисел 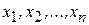называется -мерным арифметическим пространством и обозначается Rⁿ , а его элементы – точками пространства Rⁿ(мерными точками). Числа 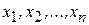при этом называют координатами точки . Точку 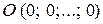называют началом координат.

 

Пусть DÌRⁿ — произвольное множество точек n-мерного арифметического пространства.

 

Определение.Числовой функцией(или отображением) 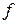от переменных, определенной на множестве D называется закон, по которому каждой точке Î D ставится в соответствие некоторое вполне определенное действительное число .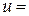

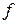
Обозначения: 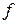:Rⁿ®R или .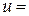

 

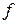
Множество D при этом называют областью определения, а множество

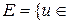R |, D}— множеством значений функции =.

 

В частном случае при функцию двух переменных можно рассматривать как функцию точек плоскости.

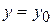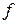
Частное значение функции при , обозначают , , 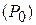и т.д.

Функция двух переменных и 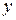может быть задана аналитическим, табличным, графическим, программным (алгоритмом вычисления 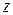по значениям и 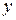) и другими способами.

Функцию двух переменных можно изобразить в трехмерном пространстве при выбранной декартовой системе координат как множество точек пространства ÎR³, координаты которых удовлетворяют уравнению , которое, вообще говоря, есть уравнение некоторой поверхности в R³. Проекцией этой поверхности на плоскость является область определения D. Каждый перпендикуляр к плоскости пересекает поверхность не более чем в одной точке (в силу однозначности функции).

 

Замечание.Функцию трех и более переменных изобразить графически невозможно.

Пример. Найти область определения функции .

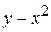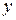Решение.Аналитическое выражение имеет смысл при любых действительных значениях и . Следовательно, областью определения является вся числовая плоскость т.е. D=R² .

Пример. Найти область определения функции .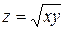

Решение.Аналитическое выражение 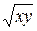имеет смысл при , следовательно, областью определения этой функции являются I и III четверти плоскости , включая ос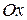и и , т.е. область, заштрихованная на рисунке.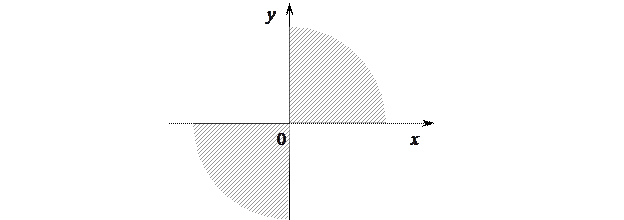

Пример. Найти область определения функции .

Решение.Для того, чтобы 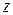имело действительное значение, необходимо, чтобы под корнем было неотрицательное число, т.е. и 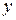должны удовлетворять неравенству или .

Все точки , координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга, т.е. область, заштрихованная на рисунке.

Пример. Найти область определения, множество значений функции , построить график.

Решение.Область определения этой функции D=R²,множество значенийЕ. Графиком данной функции в пространстве R³является параболоид вращения.

Пример. Найти область определения и множество значений функции .

Решение.Данная функция определена, если или , откуда D{R³ | }, т. е. областью определения Dданной функции является множество точек открытого трёхмерного шара радиуса , а Е(.