Дипломатия - служба, наука, искусство.
КУПА
Черга
Стек
Стек в інформатиці та програмуванні – це різновид лінійного списку, структура даних, яка працює за принципом “останнім прийшов - першим пішов” (LIFO: last in, first out). Всі операції (наприклад, видалення елементу) в стеку можна проводити тільки з одним елементом, який знаходиться на верхівці стеку та був введений в стек останнім.
Стек можна розглядати як певну аналогію до стопки тарілок, з якої можна взяти верхню, і на яку можна покласти верхню тарілку (інша назва стеку – “магазин”, за аналогією з принципом роботи магазину в автоматичній зброї).
9.2.1 Операції зі стеком
Push (“заштовхнути елемент”): елемент додається в стек та розміщується в його верхівці. Розмір стеку збільшуеться на одиницю. При перевищенні розміра стека граничної величини, відбувається переповнення стека (stack overflow)
pop (“виштовхнути елемент”): отримує елемент з верхівки стеку. При цьому він видаляється зі стеку і його місце в верхівці стеку займає наступний за ним елемент (відповідно до правила LIFO), а розмір стеку зменшується на одиницю. При намаганні “виштовхнути” елемент з вже пустого стеку, відбувається ситуація “незаповнення” стеку (stack underflow).
Кожна з вищевказаних операцій зі стеком виконується за фіксований час Т(1) і не залежить від розміру стеку.
9.2.2 Додаткові операції зі стеком (присутні не у всіх реалізаціях стеку)
ІsEmpty - це перевірка наявності елементів в стеку. Результат: істина (true), коли в стеку немає елементів.
ІsFull - це перевірка заповненості стека. Результат: істина, коли додавання нового елементу неможливе.
Сlear: звільнити стек (видалити усі елементи).
Тop: отримати верхній елемент (без виштовхування).
Size: отримати розмір (кількість елементів) стека.
Swap: поміняти два верхніх елементи місцями.
9.2.3 Організація в пам'яті комп'ютера
Стек може бути організований як масив або множина комірок в певній області комп'ютера з додатковим зберіганням ще й вказівника на верхівку стека. Заштовхування першого елемента в стек збільшує адресу вказівника, виштовхування елементу зменшує її. Таким чином, адреса вказівника завжди відповідає комірці масиву, в якій зараз знаходиться верхівка стеку.
Багато процесорів ЕОМ мають спеціалізовані регістри, які використовуються як вказівники на верхівку стеку, або використовують деякі з регістрів загального вжитку для цієї спеціальної функції в певних режимах адресації пам'яті.
9.2.4 Приклади застосування стеків
Калькулятори, які використовують зворотню нотацію, використовують стек для збереження даних обчислень.
Існує велика кількість “стеко-орієнтованих” мов програмування (Forth, PostScript), які використовують стек як базову структуру даних при виконанні багатьох операцій (арифметичних, логічних, вводу-виводу тощо).
Стеко-орієнтованими є багато з віртуальних машин, наприклад віртуальна машина Java.
Компілятори мов програмування використовують стек для передавання параметрів в процесі виклику підпрограм, процедур та функцій. Спеціалізований стек використовується також для збереження адрес повернення з підпрограм.
9.2.5 Реалізація базових алгоритмів
На високорівневих мовах програмування, стек може бути реалізований за допомогою масиву та додаткової змінної.
Для зберігання елементів стеку резервується масив S[1..n] певного розміру та додаткова змінна top[S], яка буде зберігати індекс верхівки стеку.
Операції push та pop тоді можуть бути записані так (без перевірки на переповнення та “незаповнення”):
PUSH (S, x)
1 top[S]:= top[S]+1 //збільшення індексу на 1
2 S[top[S]]:=x //запис нового елемента у верхівку стека
POP (S)
1 top[S]:=top[S]-1 // зменшення індексу на 1
2 return S[top[S]+1] //повернення колишньої верхівки стеку
Черга в програмуванні – динамічна структура даних, що працює за принципом “перший прийшов - перший пішов” (FIFO: first in, first out). У черги є голова (head) та хвіст (tail). Елемент, що додається до черги, опиняється в її хвості. Елемент, що видаляється з черги, знаходиться в її голові.
Така черга повністю аналогічна звичній “базарній” черзі, в якій хто перший встав в неї, той першим буде обслуженим (але, на відміну від реальної черги, імовірність пройти поза чергою виключена).
9.3.1 Основні операції з чергою
Еnqueue – “поставити в чергу”. Операція додавання елемента в “хвіст” черги. При цьому довжина черги збільшується на одиницю. Якщо відбувається намагання додати елемент у вже заповнену чергу, відбувається її переповнення (queue overflow).
Dequeue – “отримання з черги”. Операція, яка повертає елемент з голови та видаляє його з черги, таким чином встановлюючи голову на наступний за видаленим елемент та зменшуючи довжину на одиницю. При намаганні видалити елемент з пустої черги, виникає ситуація “незаповнення” (queue underflow).
9.3.2 Реалізація черги на мовах програмування
Черга може бути реалізована за допомогою масива Q[1...n], в якому зберігаються дані та двох додаткових змінних head[Q] та tail[Q], в яких зберігаються індекси відповідно “голови” та “хвоста” черги, lenght[Q] – довжина черги.
Тоді операції enqueue та dequeue запишуться так:
ENQUEUE (Q, x)
1 Q[tail[Q]] := x
2 if tail[Q] = length[Q]
3 then tail[Q] := 1
4 else tail[Q] := tail[Q] + 1
DEQUEUE (Q)
1 x := Q[head[Q]]
2 if head[Q] = length[Q]
3 then head[Q] := 1
4 else head[Q] := head[Q] + 1
5 return x
9.4 Зв'язаний список
Зв'язаний список в програмуванні – це одна з найважливіших структур даних, в якій елементи лінійно впорядковані, але порядок визначається не номерами елементів, а вказівниками, які входять в склад елементів списку та вказують на наступний за даним елемент (в однозв'язаних або однобічно зв'язаних списках) або на наступний та попередній елементи (в двозв'язаних або двобічно зв'язаних списках). Список має “голову” – перший елемент та “хвіст” – останній елемент.
Зв'язані списки мають серію переваг порівняно з масивами. Зокрема, в них набагато ефективніше (за час T(1), тобто незалежно від кількості елементів) виконуються процедури додавання та вилучення елементів. Натомість, масиви набагато кращі в операціях, які потребують безпосереднього доступу до кожного елементу, що у випадку зі зв'язаними списками неможливо та потребує послідовного перебору усіх елементів, які передують даному.
В однобічно зв'язаному списку, який є найпростішим різновидом зв'язаних списків, кожний елемент складається з двох полів: даних (data), та вказівника на наступний елемент (next). Якщо вказівник не вказує на інший елемент (інакше: next = NULL), то вважається, що даний елемент – останній в списку.
В двобічно зв'язаному списку елемент складається з трьох полів: вказівника на попередній елемент (prev), поля даних (data) та вказівника на наступний елемент (next). Якщо prev=NULL, то в елемента немає попередника (тобто він є “головою” списку), якщо next=NULL, то в нього немає наступника (“хвіст” списка).
В кільцевому списку перший та останній елемент зв'язані. Тобто, поле prev голови списка вказує на хвіст списка, а поле next хвоста списка вказує на голову списка.
Списки інтенсивно застосовуються в програмуванні як самостійні структури. Також на їх основі можуть будуватись більш складні структури даних, такі як дерева. На базі списків також можуть бути реалізовані стеки та черги.
В загальному випадку, якщо необхідно оперувати з динамічними множинами, де присутні інтенсивні операції з додавання або видалення елементів, існують досить переконливі аргументи для використання саме зв'язаних списків.
9.5 Зв'язані списки та масиви
Списки мають деякі переваги над масивами. Вони досить ефективні щодо операцій додавання або видалення елементу в довільному місці списка, виконуючи їх за постійний час, тоді як масиви для цього потребують часу Т(n), тобто час зростає з ростом кількості елементів масиву.
В списках також не існує проблеми “розширення”, яка рано чи пізно виникає в масивах фіксованого розміру, коли виникає необхідність включити в нього додаткові елементи. Точно так, фіксований масив, з якого було видалено багато елементів (або вони просто не використовуються) є дуже неефективним з точки зору використання пам’яті. Функціонування списків можливо в ситуації, коли пам’ять комп’ютера фрагментована, тоді як масиви переважно потребують неперервної області для зберігання.
З іншого боку, масиви дозволяють безпосередній доступ до будь-якого елементу. Однобічно зв'язані списки, натомість, потребують проходження усіх попередніх елементів. Це призводить до складнощів застосування списків в задачах, де необхідно швидко знаходити елемент за його індексом, наприклад в алгоритмах сортування. Кешування списків в таких випадках майже не дає ефекту.
Іншим очевидним недоліком списків є необхідність разом з корисною інформацією додаткового збереження інформації про вказівники, що позначається на ефективності використання пам'яті цими структурами.
9.6 Двобічне та однобічне зв'язування
Двобічне зв'язування потребує більше пам'яті на елемент та більших обчислювальних затрат на виконання елементарних операцій. Але такими списками легше маніпулювати, тому що вони дозволяють проходження по списку в обох напрямах, що є необхідною умовою функціонування деяких алгоритмів.
Контрольні запитання
1 Що таке “лінійний список” в інформатиці та програмуванні?
2 Які операції виконуються з лінійними списками?
3 Які окремі випадки лінійних списків, в яких операції додавання та вилучення певних значень можуть бути виконані лише для першого чи останнього елементу, Вам відомі?
4 Що таке “стек” в інформатиці та програмуванні?
5 Які основні операції зі стеком Вам відомі?
6 Які додаткові операції зі стеком Вам відомі?
7 Для чого використовують стек компілятори мов програмування?
8 Що таке “черга” в програмуванні?
9 Які основні операції з чергою?
10 Що таке “зв'язаний список” в програмуванні?
11 Які є різновиди зв'язаних списків?
12 Де застосовуються списки?
13 Які Переваги та недоліки списків?
14 В чому полягає відмінність зв'язаних списків та масивів?
Лекція №10
ЗБЕРЕЖЕННЯ І СОРТУВАННЯ МАСИВІВ ДАНИХ
Однією з переваг масивів є можливість компактного збереження послідовності їх елементів в локальній області пам'яті (що не завжди вдається, наприклад, для зв'язаних списків), що дозволяє ефективно виконувати операції з послідовного обходу елементів таких масивів.
Масиви є дуже економною щодо пам'яті структурою даних. Для збереження 100 цілих чисел в масиві необхідно рівно в 100 разів більше пам'яті, ніж для збереження одного числа (плюс, можливо, ще декілька байтів). В той же час, усі структури даних, які базуються на вказівниках, потребують додаткової пам'яті для збереження самих вказівників разом з даними. Однак, операції з фіксованими масивами ускладнюються тоді, коли виникає необхідність додавання нових елементів у вже заповнений масив. Тоді його необхідно розширювати, що не завжди можливо і для таких задач слід використовувати зв'язані списки, або динамічні масиви.
У випадках, коли розмір масиву є досить великий та використання звичайного звертання за індексом стає проблематичним, або великий відсоток його комірок не використовується, слід звертатись до асоціативних масивів, де проблема індексування великих об'ємів інформації вирішується більш оптимально.
Оскільки масиви мають фіксовану довжину, слід дуже обережно ставитись до процедури звертання до елементів за їхнім індексом, тому що намагання звернутись до елементу, індекс якого перевищує розмір такого масива (наприклад, до елементу з індексом 6 в масиві з 5 елементів), може призвести до непередбачуваних наслідків.
Слід також бути уважним щодо принципів нумерації елементів масиву, яка в одних мовах програмування може починатись з 0, а в інших – з 1.
Збереження одновимірного масиву в пам'яті є тривіальним, тому що сама пам'ять комп'ютера є одновимірним масивом. Для збереження багатовимірного масиву ситуація ускладнюється.
Найпоширеніші способи його організації в пам'яті такі:
- розташування “рядок за рядком”. Це найбільш уживаний на сьогодні спосіб, який зустрічається у більшості мов програмування (1 2 3 4 5 6 7 8 9);
- розташування “стовпчик за стовпчиком”. Такий метод розташування масивів використовується, зокрема, в мові програмування Fortran (1 4 7 2 5 8 3 6 9).
Масив з масивів. Багатовимірні масиви репрезентуються одновимірними масивами вказівників на одновимірні масиви. Розташування може бути як “рядок за рядком” так і “стовпчик за стовпчиком”.
Перші два способи дозволяють розміщувати дані компактніше (мають більшу локальність), однак це одночасно і обмеження: такі масиви мають бути “прямокутними”, тобто кожний рядок повинен містити однакову кількість елементів. Розташування “масив з масивів”, з іншого боку, не дуже ефективне щодо використання пам'яті (необхідно зберігати додатково інформацію про вказівники), але знімає обмеження на “прямокутність” масиву.
Контрольні запитання
1 В чому полягає перевага масивів в порівнянні з списками?
2 З якого числа починається нумерація елементів масиву в різних мовах програмування?
3 Як в пам’яті комп’ютера відбувається збереження багатовимірного масиву?
4 В чому перевага “масиву з масивів”?
Лекція №11
ДЕРЕВО. БІНАРНЕ ДЕРЕВО ПОШУКУ
Дерево - в інформатиці та програмуванні одна з найпоширеніших структур даних. Формально дерево визначається як скінченна множина Т з однієї або більше вершин (вузлів, nodes), яка задовольняє наступним вимогам:
- існує один особливий вузол - корінь дерева (root);
- інші вузли (за виключенням кореня) розподілені серед m ≥ 0 непересічних множин T1...Tm і кожна з цих множин в свою чергу є деревом. Дерева T1...Tm мають назву піддерев (subtrees) даного кореня.
З цього визначення випливає, що кожна вершина є в свою чергу коренем деякого піддерева. Кількість піддерев вершини має назву ступеня (degree) цієї вершини. Вершина ступеню нуль має назву кінцевої (terminal) або листа (leaf). Некінцева вершина також має назву вершини розгалуження (branch node). Нехай x - довільна вершина дерева з коренем r. Тоді існує єдиний шлях з r до x. Усі вершини на цьому шляху називаються предками (ancestors) x. Якщо деяка вершина y є предком x, то x називається нащадком (descendant) y. Нащадки та предки вершини x, що не співпадають з нею самою, називаються власними нащадками та предками. Кожну вершину x, в свою чергу, можна розглядати як корінь деякого піддерева, елементами якого є вершини-нащадки x. Якщо вершини x є предками y та не існує вершин поміж ними (тобто x та y з'єднані одним ребром), а також існують предки для x (тобто x не є коренем), то вершина x називається батьком (parent) до y, а y - дитиною (child) x. Коренева вершина єдина не має батьків. Вершини, що мають спільного батька, називаються братами (siblings). Вершини, що мають дітей, називаються внутрішніми (internal). Глибиною вершини x називається довжина шляху від кореня до цієї вершини. Максимальна глибина вершин дерева називається висотою.
Якщо існує відносний порядок на піддеревах T1...Tm, то таке дерево називається впорядкованим (ordered tree) або пласким (plane tree).
Лісом (forest) називають множину дерев, які не перетинаються.
Найчастіше дерева в інформатиці зображують з коренем, який знаходиться зверху (говорять, що дерево в інформатиці “росте вниз”).
Важливим окремим випадком кореневих дерев є бінарні дерева, які широко застосовуються в програмуванні і визначаються як множина вершин, яка має виокремлений корінь та два піддерева (праве та ліве), що не перетинаються, або є пустою множиною вершин (на відміну від звичайного дерева, яке не може бути пустим).
Важливими операціями над деревами є:
- обхід вершин в різному порядку;
- перенумерація вершин;
- пошук елемента;
- додавання елемента у визначене місце в дереві;
- видалення елемента;
- видалення цілого фрагмента дерева;
- додавання цілого фрагмента дерева;
- трансформації (повороти) фрагментів дерева;
- знаходження кореня для будь-якої вершини.
Найбільшого розповсюдження ці структури даних набули в тих задачах, де необхідне маніпулювання з ієрархічними даними, ефективний пошук в даних, їх структуроване зберігання та модифікація.
11.1 Бінарне дерево
В програмуванні бінарне дерево – це дерево структури даних, в якому кожна вершина має не більше двох дітей. Зазвичай такі діти називаються правим та лівим. На базі бінарних дерев будуються такі структури, як бінарні дерева пошуку та бінарні купи.
На рис.11.1 показана узагальнена структура бінарного дерева.

Рисунок 11.1 – Узагальнена структура бінарного дерева
Різновиди бінарних дерев:
- бінарне дерево (кореневе дерево, в якому кожна вершина має не більше двох дітей);
- повне (закінчене) бінарне дерево (бінарне дерево, в якому кожна вершина має нуль або двох дітей);
- ідеальне бінарне дерево – це повне бінарне дерево, в якому листя (вершини без дітей) лежать на однаковій глибині (відстані від кореня).
Бінарне дерево на кожному n-му рівні має від 1 до 2n вершин.
Часто виникає необхідність обійти усі вершини дерева для аналізу інформації, що в них знаходиться. Існують декілька порядків такого обходу, кожний з яких має певні властивості, важливі в тих чи інших алгоритмах:
- прямий (preorder);
- центрований (inorder);
- зворотній (postorder).
Реалізація бінарного дерева показана на рис11.2. Кожна вершина містить вказівники на праву та ліву дитину (left та right).
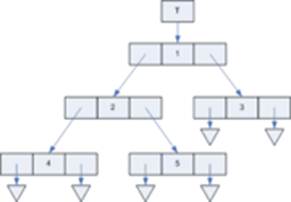
Рисунок 11.2 – Реалізація бінарного дерева
Існують декілька варіантів конструювання бінарних дерев в залежності від задач, які вирішуються цими структурами та можливостей тої чи іншої мови програмування. Реалізація з використанням вказівників передбачає зберігання в кожній вершині дерева x разом з даними двох полів з вказівниками (правим та лівим) right[x] та left[x] на відповідних дітей цієї вершини (рис.11.3).
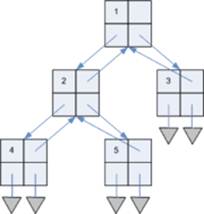
Рисунок 11.3 – Реалізація бінарного дерева з використанням вказівників
Модифікована реалізація бінарного дерева. Кожна вершина містить також вказівник на батьківську вершину
Також іноді додається вказівник p[x] на батьківську вершину. Це виявляється корисним, коли необхідний швидкий доступ до батьківської вершини, що спрощує деякі алгоритми. Іноді достатньо тільки вказівника на батьківську вершину. Взагалі будь-яке орієнтоване дерево можна описати, знаючи тільки зв'язки від дітей до батьківської вершини. Деякі різновиди бінарних дерев (наприклад, червоно-чорні дерева або AVL-дерева), вимагають збереження в вершинах і деякої додаткової інформації. Якщо у вершини відсутня одна чи обидві дитини, відповідні вказівники ініціалізуються спеціальними “порожніми” значеннями.
Бінарні дерева також можуть бути побудовані на базі масивів (рис.11.4). Такий метод набагато ефективніший щодо економії пам'яті. В такому представленні, якщо вершина має порядковий номер i, то її діти знаходяться за індексами 2i+1 та 2i+2, а батьківська вершина за індексом ((i-1)/2) (за умов, що коренева вершина має індекс 0).
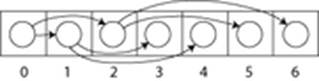
Рисунок 11.4 – Бінарні дерево побудоване на базі масиву
Інший варіант збереження дерева в масиві – це збереження індексів дітей.
Існує єдине та взаємооднозначне відображення довільного впорядкованого дерева в бінарне (рис.11.5).
Для цього слід послідовно зв'язати усіх дітей кожної сім'ї з першою дитиною та та видалити усі вертикальні з'єднання за виключенням з'єднання батька з першою дитиною в сім'ї. Тобто кожна вершина N впорядкованого дерева відповідає вершині M деякого бінарного дерева. Ліва дитина вершини M відповідає першій дитині вершини N, а права дитина M відповідає першому з наступних братів N (тобто першому з наступних дітей батька вершини N).
Така відповідність має назву природної відповідності між впорядкованим та бінарним деревом.
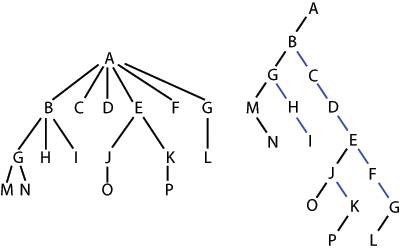
Рисунок 11.5 – Відображення довільного впорядкованого дерева в бінарне
Бінáрне дéрево пóшуку (BST: binary search tree) в інформатиці – це бінарне дерево, в якому кожній вершині x співставлене певне значення val[x]. При цьому такі значення повинні задовольняти умові впорядкованості:
- нехай x – це довільна вершина бінарного дерева пошуку. Якщо вершина y знаходиться в лівомі піддереві вершини x, то val[y] ≤ val[x]. Якщо у знаходиться у правому піддереві x, то val[y] ≥ val[x].
Таке структурування дозволяє надрукувати усі значення у зростаючому порядку за допомогою простого алгоритма центрованого обходу дерева. Бінарні дерева пошуку набагато ефективніші в операціях пошуку, аніж лінійні структури, в яких витрати часу на пошук пропорційні Т(n), де n – це розмір масиву даних, тоді як в повному бінарному дереві цей час пропорційний в середньому Т(log2n) або Т(h), де h - висота дерева (хоча гарантувати, що h не перевищує log2n можна лише для збалансованих дерев, які є ефективнішими при пошукових алгоритмах, ніж прості бінарні дерева пошуку).
Процедура пошуку в бінарному дереві отримує на вході значення k, яке необхідно знайти, та вказівник x на корень того піддерева, в якому слід шукати.
SEARCH (x, k)1 if x = NULL or k = val[x]2 then return x3 if k < val[x] 4 then return SEARCH (left[x], k)5 else return SEARCH (right[x], k)В процесі пошуку ми рухаємось від кореня, порівнюючи значення kзі значенням в поточній вершині х. Якщо k < val[x], пошук рекурсивно продовжується в лівому піддереві (kможе бути тільки там згідно умови впорядкованості), інакше - у правому піддереві. Очевидно, що довжина шляху не перевищує висоти дерева, тому час пошуку є Т(h), де h - висота дерева.
Мінімальний елемент в дереві можна знайти, розглянувши послідовно ліве піддерево left[x]:
MINIMUM (x)1 while left[x]<>NULL2 do x:=left[x]3 return xПроцедура знаходження максимуму симетрична. Обидві процедури знову ж таки знаходять елемент за час, пропорційний Т(h)
Елемент, що є наступним за даним (в сенсі відношення впорядкованості) можна знайти за допомогою такої процедури:
SUCCESSOR (x)1 if right[x] <> NULL2 then return MINIMUM (right[x])3 y:=p[x]4 while y<>NULL and x = right[y]5 do x:=y6 y:=p[y]7 return yПроцедура знаходження попереднього даному елементу є симетричною. Обидві процедури знову ж таки знаходять елемент за час, пропорційний Т(h)
Процедура додавання елементу в бінарне дерево T додає елемент, зберігаючи умову впорядкованості. Параметром тут є вказівник z на нову вершину, в якій розміщене значення val[z], left[z]=right[z]=NULL:
INSERT (T, z)1 y:=NIL2 x:=root[T]3 while x <> NULL 4 do y:=x5 if val[z] < val[x]6 then x:=left[x]7 else x:=right[x]8 p[z]:=NULL9 if y = NULL10 then root[T] :=z11 else if val[z]<val[y]12 then left[y]:=z13 else right[y]:=zПроцедура рухається вниз по дереву, при цьому зберігаючи в yвказівник на батька вершини x. Порівнюючи значення в x та z, процедура вирішує, в яке з піддерев рухатись далі. Процес завершується тоді, коли x=NULL. Саме сюди й слід помістити вершину z (рядки 8-13). Ця операція також потребує часу для виконання, пропорційного Т(h)
Параметром для процедури видалення елементу є вказівник на вершину, що видаляється. Тут можливі три варіанти дій:
- якщо у вершини немає дітей, достатньо помістити NULL у відповідне поле його батька (замість вказівника на вершину, що видаляється);
- якщо у вершини є одна дитина, можна з'єднати батька цієї вершини безпосередньо з її дитиною;
- якщо вершина має двох дітей, слід спочатку знайти слідуючий (в сенсі порядку) елемент y, в якого немає лівої дитини, а потім скопіювати значення та додаткові дані з вершини y на місце вершини, що видаляється, а саму вершину yвидалити:
DELETE (T, z)1 if left[z] = NULL or right[z]=NULL 2 then y:=z3 else y:=SUCCESSOR(z)4 if left[y] <> NULL 5 then x:=left[y]6 else x:= right[y]7 if x <> NULL8 then p[x]:=p[y]9 if p[y]:=NULL10 then root[T]:=x11 else if y=left[p[y]]12 then left[p[y]] :=x13 else right[p[y]]:=x14 if y <> z15 then val[z]:=val[y]16 //копіювання додаткових даних з y17 return y
В програмуванні збалансоване дерево в загальному розумінні цього слова – це такий різновид бінарного дерева пошуку, яке автоматично підтримує свою висоту, тобто кількість рівнів вершин під коренем, мінімальною. Ця властивість є важливою тому, що час виконання більшості алгоритмів на бінарних деревах пошуку пропорційний до їх висоти, і звичайні бінарні дерева пошуку можуть мати досить велику висоту в тривіальних ситуаціях. Процедура зменшення (балансування) висоти дерева виконується за допомогою трансформацій, відомих як обернення дерева, в певні моменти часу (переважно при видаленні або додаванні нових елементів).
Більш строге визначення збалансованих дерев було дане Г.Адельсон-Вельським та Є.Ландісом. Ідеально збалансованим деревом за Адельсон-Вельським та Ландісом є таке, у якого для кожної вершини різниця між висотами лівого та правого піддерев не перевищує одиниці. Однак, така умова доволі складна для виконання на практиці і може вимагати значної перебудови дерева при додаванні або видаленні елементів.
Тому було запропоноване менш строге визначення, яке отримало назву умови АВЛ(AVL)-збалансованості і говорить, що бінарне дерево є збалансованим, якщо висоти лівого та правого піддерев різняться не більше ніж на одиницію. Дерева, що задовольняють таким умовам, називаються AVL-деревами. Зрозуміло, що кожне ідеально збалансоване дерево є також АВЛ-збалансованим, але не навпаки.
Червоно-чорне дерево (red-black tree) в інформатиці – це різновид бінарного дерева пошуку, вершини якого мають додаткові властивості (RB-властивості), зокрема “колір” (червоний або чорний). Червоно-чорні дерева – це різновид збалансованих дерев, в яких за допомогою спеціальних трансформацій гарантується, що висота дерева h не буде перевищувати Т(log n). Зважаючи на те, що час виконання основних операцій на бінарних деревах (пошук, видалення, додавання елементу) є Т(h), ці структури даних на практиці є набагато ефективнішими, аніж звичайні бінарні дерева пошуку.
Бінарне дерево називається червоно-чорним, якщо воно має наступні властивості (рис.11.6):
- кожна вершина або червона, або чорна;
- корінь дерева – чорний;
- кожний лист (NIL) – чорний;
- якщо вершина червона, обидві її дитини чорні;
- усі шляхи від кореня до листків, мають однакову кількість чорних вершин.
Такі властивості надають червоно-чорному дереву додаткового обмеження: найдовший шлях з кореня до будь-якого листа перевищує найкоротший шлях не більше ніж в двічі. В цьому сенсі таке дерево можна назвати збалансованим. Зважаючи на те, що час виконання основних операцій з бінарними деревами пошуку залежить від висоти, таке обмеження гарантує їхню ефективність в найгіршому випадку, чого звичайні бінарні дерева гарантувати не можуть.
Для того, щоб зрозуміти, чому перелічені властивості забезпечують існування такого обмеження, зазначимо, що в червоно-чорному дереві, відповідно до властивості “якщо вершина червона, обидві її дитини чорні” не існує такого шляху, на якому б зустрілись дві червоні вершини підряд. Найкоротший шлях складається з усіх чорних вершин, а в найдовшому червоні та чорні вершини чергуються. З врахуванням властивості “усі шляхи від кореня до листків, мають однакову кількість чорних вершин”, отримуємо, що глибина будь-яких двох листів відрізняється не більше ніж в два рази.
В деяких зображеннях червоно-чорних дерев, NIL-листя не наводяться, тому що вони не містять корисної інформації, але їх існування необхідне для забезпечення усіх властивостей.

Рисунок 11.6 – Бінарне червоно-чорне дерево
Операції, які не пов'язані з модифікацією RB-дерева, не потребують коректив і повністю аналогічні відповідним операціям для звичайних бінарних дерев пошуку. Разом з тим, додавання або видалення елементу з червоно-чорного дерева може призвести до порушення RB-властивостей. Відновлення цих властивостей після модифікації дерева потребує порівняно невеликої кількості (Т(log n)) операцій зі зміни кольору вершин та не більше як трьох операцій повороту (дві при додаванні елементу). Це залишає часові параметри операцій додавання та видалення в межах Т(log n), але ускладнює відповідні алгоритми.
Процедура вставки елементу починається аналогічно вставці елементу в бінарне дерево пошуку та фарбування його у червоний колір. Подальші дії залежать від кольорів сусідніх вершин. Зазначимо, що:
- властивість 2 завжди зберігається;
- властивість 3 порушується тільки при вставці червоної вершини, перефарбуванні чорної вершини в червону або обертанні;
- властивість 4 порушується тільки при вставці чорної вершини, перефарбувані червоної вершини в чорну або обертанні.
На допоміжних рисунках, вершина, яка додається, позначена N, первісний батько цієї вершини позначений P, батько вершини P (“дідусь” N) позначений G. “Дядько” N (тобто вершина, яка має спільного з P батька - G) позначений як U. Розглянемо наступні приклади.
Приклад 1(рис.11.7): нова вершина знаходиться в корені дерева. В такому випадку необхідно пофарбувати її в чорний колір для забезпечення властивості 1. Очевидно, що властивість 5 при цьому залишається справедливою.
Приклад 2(рис.11.7): Батько нової вершини є чорним. Властивість 3 не порушена. В цьому випадку дерево є коректним. Властивість 5 також зберігається, адже червона вершина додається на місце чорного листа і це не змінює кількості чорних вершин на цьому шляху.
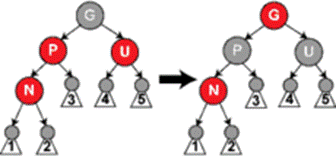 Рисунок 11.7 – Проведення змін в бінарному червоно-чорному дереві
Приклад 3: Батько та дядько доданої вершини є червоними. Тоді ми можемо перефарбувати їх обох в чорний, а також перефарбувати дідуся в червоний. Тепер наша червона вершина має чорного батька. Завдяки тому, що будь-який шлях через батька чи дядька повинен проходити і через дідуся, кількість чорних вершин на шляху залишається незмінною. Однак батько дідуся (тобто прадідусь) може бути червоною вершиною, як тепер і дідусь. Якщо це так, слід повторити цю операцію рекурсивно.
Рисунок 11.7 – Проведення змін в бінарному червоно-чорному дереві
Приклад 3: Батько та дядько доданої вершини є червоними. Тоді ми можемо перефарбувати їх обох в чорний, а також перефарбувати дідуся в червоний. Тепер наша червона вершина має чорного батька. Завдяки тому, що будь-який шлях через батька чи дядька повинен проходити і через дідуся, кількість чорних вершин на шляху залишається незмінною. Однак батько дідуся (тобто прадідусь) може бути червоною вершиною, як тепер і дідусь. Якщо це так, слід повторити цю операцію рекурсивно.
|
В наступних випадках ми припускаємо, вершина P є лівою дитиною G. Якщо P - права дитина, ліво та право в аналізі наступних випадків слід поміняти місцями.
Приклад 4(рис.11.8): батько є червоним, але дядько - чорний. До того ж, нова вершина - права дитина свого батька, і батько в свою чергу ліва дитина свого батька. В такому випадку, ми можемо провести лівий поворот, внаслідок якого нова вершина та її батько поміняються ролями. Подальші дії з бувшим батьком проводяться відповідно до випадку 5. Зважаючи на те, що нова вершина та її батько є червоними, операція повороту не змінює умови 4.
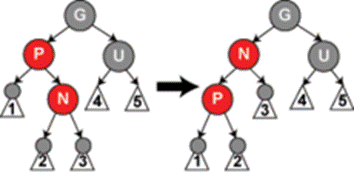 Рисунок 11.8 – Проведення змін в бінарному червоно-чорному дереві
Рисунок 11.8 – Проведення змін в бінарному червоно-чорному дереві
|
| Приклад 5(рис.11.9): батько є червоним, але дядько чорний. До того ж, нова вершина - ліва дитина свого батька, і батько є лівою дитиною свого батька. В такому випадку ми проводимо правий поворот навколо дідуся. В результаті бувший батько тепер є батьком і нової вершини, і свого бувшого дідуся. Ми знаємо, що бувший дідусь є чорним, інакше б батько не був червоним. Тепер слід поміняти місцями кольори бувшого батька та дідуся, і тепер дерево виконує властивість 3. Легко бачити, що властивість 4 також залишається незмінною. |

Рисунок 11.9 – Проведення змін в бінарному червоно-чорному дереві
Контрольні запитання
1 Що таке “дерево” в інформатиці та програмуванні?
2 Яку множину “дерев” в інформатиці та програмуванні називають “лісом”?
3 В чому ” в інформатиці та програмуванні полягає відмінність “бінарного дерева” від “звичайного дерева”?
4 Які є різновиди бінарних дерев?
5 В чому полягає особливість реалізації бінарного дерева з використанням вказівників?
6 Що в програмуванні розуміють під терміном “збалансоване дерево”?
Лекція №12
Купа або піраміда (heap) в інформатиці – це спеціалізована деревовидна структура даних, в якій існують певні властивості впорядкованості. Така структура даних повинна задовільняти основній властивості купи: нехай А та B є елементами купи, такими, що B підпорядковане A (B – це дитина А). Тоді значення B не повинно перевищувати А, тобто val[B] ≤ val[A].
Найбільш уживаним класом куп є бінарні купи.
Базові операції з купою такі:
- підтримка основної властивості купи;
- побудова купи з невпорядкованого масиву;
- сортування купи;
- видалення найменшого елемента;
- отримання найбільшого елемента;
- додавання елемента.
Купи часто використовуються для моделювання черг з пріоритетами.
Бінарна купа (binary heap) – це структура даних, що є масивом, який можна розглядати як майже повне бінарне дерево. Кожен вузол цього дерева відповідає певному елементу масиву. На всіх рівнях, крім, можливо останнього, дерево повністю заповнене (заповнений рівень – це такий, що містить максимально можливу кількість вузлів). Останній рівень заповнюється послідовно зліва направо до тих пір, доки в масиві не закінчаться елементи.
Для масиву A у корені дерева знаходиться елемент A[1]. Далі дерево будується за наступним принципом: якщо якомусь вузлу відповідає індекс i, то індекс його батьківського вузла обчислюється за допомогою процедури Parent(i), індекс лівого дочірнього вузла знаходиться за допомогою процедури Left(i), а індекс правого дочірнього вузла визначається за допомогою процедури Right(i):
Parent(i) return [i/2] Left(i) return 2i Right(i) return 2i + 1Розглядають два види бінарних куп: неспадні і незростаючі. В обох видах значення, що розташовані у вузлах купи, задовільняють властивості купи (heap property). Властивість незростаючої купи (max-heap property) полягає в тому, що для кожного вузла крім кореневого виконується нерівність:
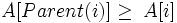 .
.
Іншими словами, значення вузла не перевищує значення батьківського вузла. Таким чином найбільший елемент знаходиться в корені дерева. Принцип побудови неспадної купи(min-heap) протилежний. Властивість неспадної купи (min-heap property) полягає в тому, що кожен елемент крім кореневого є неменшим за свій батьківський елемент:
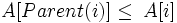 .
.
Підтримку властивості купи можна здійснювати за допомогою процедури Max_Heapify (для незростаючих бінарних куп). На вхід подається масив A й індекс i цього масиву. При виклику процедури Max_Heapify припускається, що бінарні дерева, коренями яких є елементи Left(i) і Right(i) є незростаючими купами, але сам елемент A[i] може бути меншим за його дочірні елементи і тим самим порушувати властивість незростаючої купи. Процедура Max_Heapify спускає значення елемента A[i] вниз по купі до тих пір, доки дерево в якому цей елемент буде корнем не стане незростаючою бінарною купою:
Max_Heapify(A,i) 1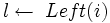 2
2 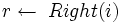 3 if
3 if  і A[l] > A[i] 4 then
і A[l] > A[i] 4 then 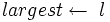 5 else
5 else 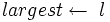 6 if
6 if  і A[r] > A[largest] 7 then
і A[r] > A[largest] 7 then 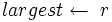 8 if
8 if 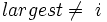 9 then Поміняти
9 then Поміняти 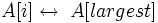 10 Max_Heapify(A,largest)
10 Max_Heapify(A,largest) Час роботи процедури в найгіршому випадку пропорційний висоті купи. Якщо купа складається з n елементів, то її висота log2(n) . Тому оцінка часу роботи одного визову Max_Heapify є Т(log n).
Для падтримки властивості неспадної бінарної купи можна скористатись процедурою Min_Heapify. Вона повністю подібна до Max_Heapify, тільки в рядках 3 і 6 алгоритму знак ">" треба замінити на "<".
За допомогою процедури Max_Heapify можно перетворити масив A[1..n], де n = length[A], у незростаючу купу. Всі елементи підмасиву 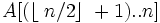 є листами дерева, тому кожен з них можна вважати одноелементною купою, з якої можна почати процес побудови. Процедура Build_Max_Heap проходить по всім іншим вузлам і для кожного з них виконує процедуру Max_Heapify:
є листами дерева, тому кожен з них можна вважати одноелементною купою, з якої можна почати процес побудови. Процедура Build_Max_Heap проходить по всім іншим вузлам і для кожного з них виконує процедуру Max_Heapify:
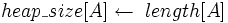 2 for
2 for 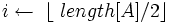 downto 13 do Max_Heapify(A,i)
downto 13 do Max_Heapify(A,i) По завершенню роботи процедури, масив A організується в незростаючу купу. Час роботи процедури Build_Max_Heap можна записати так:
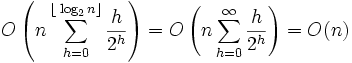
Для створення неспадної купи, необхідно замінити у третьому рядку алгоритма виклик Max_Heapify на Min_Heapify.
Робота алгоритму сортування купи починається з віклику процедури Build_Max_H, за допомогою якої з початкового масиву A[1..n] створюється незростаюча купа. Далі послідовно з купи виймається найбільший елемент, який міняють з останнім в купі. Після кожного обміну розмір купи зменшують на одиницю. В кінці отримують повністю відсортований неспадний масив:
Heapsort(A)1 Build_Max_Heap(A)2 for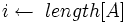 downto 23 do Поміняти
downto 23 do Поміняти 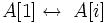 4
4 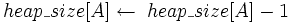 5 Max_Heapify(A,1)
5 Max_Heapify(A,1) Час роботи процедури Heapsort рівний Т(n log n), оскільки всього потрібно n-1 викликів Max_Heapify, кожен з яких працює за Т(log n).
Контрольні запитання
1 Яким терміном в інформатиці називають спеціалізовану деревовидну структуру даних, в якій існують певні властивості впорядкованості?
2 Які базові операції з купою Вам відомі?
3 Яка властивість незростаючої купи?
4 Який принцип побудови неспадної купи?
5 Яка властивість неспадної купи?
Перелік рекомендованих джерел
- Вирт, Никлаус. Алгоритмы и структуры данных. - СПб.: Невский Диалект. – 2001. – 351 с.
- Уильям Топп, Уильям Форд. Структуры данных в С++. – М.: ЗАО “Издательство БИНОМ”. – 2000. – 816 с.
- Ахо Альфред В., Хопкрофт Джон, Ульман Джеффри Д. Структуры данных и алгоритмы.: Учебное пособие. – М.: Издательский дом “Вильямс”. – 2000. – 384 с.
- Трамбле Ж., Соренсон П. Введение в структуры данных. - М.: Машиностроение. – 1982. - 784 с.
- Костюк Ю.Л. Основы алгоритмизации: Учебное пособие. - Томск: Изд.ТГУ. – 1996. - 124 с.
- Орлов В.А. Теория графов и комбинаторика: Учебное пособие. - Томск: Изд.ТПИ. – 1988. - 96 с.
- Райли Д. Абстракция и структуры данных: Вводный курс. - М.: Мир. – 1993. - 752 с.
- Брой М. Информатика. Теоретическая информатика, алгоритмы и структуры данных, логическое программирование, объектная ориентация. - М.: Диалог-МИФИ. – 1998. - 224 с.
- Евстигнеев В.А. Применение теории графов в программировании. - М.: Наука. Гл. Ред. ФМЛ. – 1985. - 352 с.
- Нечепуренко М.И., Попков В.К. Алгоритмы и программы решения задач на графах и сетях. - Новосибирск: Наука. Сиб.отделение. - 1990. - 515 с.
- Кристофидес. Н. Теория графов. Алгоритмический подход. – М.: Мир. – 1978. – 432 с.
- Оре, Ойстин. Теория графов. - М.: Наука: Физико-математическая литератураю – 1980. - 336 с.
- Пападимитриу Х., Стайглиц К.. Комбинаторная оптимизация; Алгоритмы и сложность. – М.: Мир. – 1985. - 510 с.
- Свами М., Тхуласираман К.. Графы, сети и алгоритмы. – М.: Мир. – 1984. – 454 с.
- Криницкий Н.А., Миронов Г.А., Фролов Г.Д. Автоматизированные информационные системы. - М.: Наука. - 1987.- 384с.
- Селтон Г. Автоматическая обработка, хранение и поиск информации. - М.: Сов. Радио. - 1973. - 352 с.
- Вирт. Н. Алгоритмы и структуры данных. - М.: Мир. - 1989. - 360 с.
|
|
|
|
|
|
|
Дипломатия - инструмент реализации внешнеполитического курса государства, совокупность средств, приемов и методов достижения внешнеполитических целей государства; система взаимоотношений между суверенными государствами, основанная на взаимном обмене дипломатическими представителями, воплощающими суверенитет своего государства.