МЕТОДИКА ИЗУЧЕНИЯ ЧИСЛОВЫХ ВЫРАЖЕНИЙ И ВЫРАЖЕНИЙ С ПЕРЕМЕННОЙ
МЕТОДИКА ИЗУЧЕНИЯ АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА
Числовыми выражениями называется запись, состоящая из чисел, знаков действия и скобок.
Ознакомление с числовыми выражениями предполагает 3 этапа:
1. Числовые выражения, составленные с помощью только одного действия – сложения, вычитания, умножения, деления: 5+2, 7- 4, 2*3, 10:5 и т.д.
2. Числовые выражения, составленные с помощью двух действий одной и той же ступени (сложение и вычитание – 1ступень, умножение и деление – 2ступень) и скобок: 5+2-3, 10- (3+4), 6*4:8, 36: (2*3) и т.д.
3. Числовые выражения, составленные с помощью действий разных ступеней и скобок: (27+3):10, (5+3)*2, 5*3+7, 20:4- 3 и т.д.
Цели:
1. Сформировать умение читать, записывать и сравнивать числовые выражения.
2. Познакомить с правилами выполнения действий со скобками и действий разных ступеней.
3. Выработать умение находить значение числового выражения.
4. Познакомить с тождественными преобразованиями.
Умение читать, записывать и сравнивать числовые выражении формируется в процессе работы над соответствующими операциями над числами:
§ Действие сложения связано с операцией объединения множеств.
§ Действие вычитания связано с операцией дополнения подмножеств.
Поэтому сначала дети читают выражения так: 2+1 – к двум прибавить один,
2- 1 – от двух отнять один.
После знакомства со свойствами арифметических действий: прибавить 1 – это значит увеличить число на 1, вычесть 1- уменьшить число на 1, дети читают так:
2+1 – два увеличить на 1.
2-1 – два уменьшить на 1.
Затем дети знакомятся с действием сложения, названием знака действия и названием чисел. Меняется и прочтение: 2+1 – два плюс один.
2+1 – сумма двух и одного.
2+1 – первое слагаемое 2, второе 1.
Учащиеся должны осознать, что записать сумму, это значит записать выражение с помощью соответствующего знака действия, а вычислить сумму – значит найти значение выражения, найти результат.
Для усвоения термина «сумма» используются задания:
§ Запиши сумму чисел восьми и двух.
§ Вычисли значение суммы пяти и трёх.
§ Прочитай запись 7+2.
§ Замени число 10 суммой двух чисел.
§ Сравните суммы чисел 5+3 и 4+6.
В дальнейшем дети изучают другие арифметические действия, название знаков действии и чисел. Возможны варианты прочтения:
7+4 – к 7 прибавить 4. 7-4 – из 7 вычесть 4.
- 7 увеличить на 4. - 7 уменьшить на 4.
- 7 плюс 4. – 7 минус 4.
- сумма 7 и 4. – разность 7 и 4.
- первое слагаемое 7, второе слагаемое 4. – уменьшаемое 7, вычитаемое 4.
7*4 –по 7 взять 4 раза. 16:2 – 16 уменьшили в 2 раза.
- 7 увеличить в 4 раза. - 16 разделить на 2.
-7умножить на 4. – частное 16 и 2.
- произведение 7 и 4. – делимое 16. делитель 2.
- первый множитель 7, второй множитель 4.
Затем рассматриваются выражения из трёх и более чисел, соединённых знаками действий одной ступени (5+4-3, 7-4+5). Учитель раскрывает смысл этих выражений, показывает, как найти их значение. Находя их значение, дети узнают о порядке действий и прочтении.
Знакомство с выражениями, содержащими скобки, может проходить так:
§ Учитель сразу учит детей читать готовые выражения по аналогии с образцом.
§ Учитель вместе с детьми составляет выражения.
Учитель предлагает из карточек с числами и знаками действий составить выражения, прочесть их и найти их значения. Например,
составить выражения, прочесть их и найти их значения. Например, , или
, или  .Затем составляются новые выражения из карточек
.Затем составляются новые выражения из карточек ,
, ,
, ,
,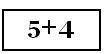 ,
, ,
, . Например,
. Например, или
или .
.
Для чтения используется памятка:
1. Посмотри на знак действия в скобках. Что записано – сумма или разность?
2. Посмотри на другой знак, вне скобок и скажи, что надо сделать.
Например, 10-(5+4) – разность десяти и суммы чисел пяти и четырёх.
- из 10 вычесть сумму чисел 5 и 4.
(6-4)+8 – сумма разности чисел шести и четырёх.
- к разности чисел 6 и 4 прибавить число 8.
Затем изучаются выражения, в которых одно или несколько слагаемых суммы заменены произведением или частным.
При знакомстве с такими выражениями учитель предлагает записать сумму 24 и 16, получают 24+16. После этого надо заменить первое слагаемое произведением, появляется запись 4*6+16, заменить второе слагаемое 24+2*8, заменить оба слагаемых 4*6+2*8. Далее выясняется, какое действие выполняется последним, и как называются компоненты этого действия. Прочтение может быть таким:
4*6+16 – сумма произведения 4 и 6 и числа 16,
- к произведению 4 и 6 прибавить 16,
- первое слагаемое представлено произведением 4 и 6, второе слагаемое – 16.
Изучение правил порядка выполнения действий в выражениях.
1. Сначала рассматривается порядок выполнения действий в выражениях без скобок, содержащих действия одной ступени (5+4-3, 7*6:2). Учащиеся находят значения этих выражений, учитель организует наблюдение и подводит к выводу: действия в выражениях без скобок, содержащие только сложение и вычитание или умножение и деление, выполняются в том порядке, в котором они записаны.
2. Далее рассматриваются выражения без скобок, в которых используются действия разных ступеней: 1ступень- сложение и вычитание, 2 ступень – умножение и деление(5*7-10, 3+4:2).сначала учитель сообщает правило: в выражениях без скобок, в которых используются действия разных ступеней, сначала выполняется умножение или деление, а потом сложение или вычитание. Уже по нему дети находят значения выражений. Важно организовать анализ выражения и выявить порядок действия.
3. Порядок действий в выражениях, содержащих скобки. Дети уже знают, как выполнять действия со скобками. Они сами находят значения выражений, плотом учитель организует наблюдение и формулирует правило: если выражение содержит скобки, то сначала действия в установленном порядке выполняются в них, а потом вне скобок.
Для закрепления можно предложить задания:
§ Измени порядок действий с помощью скобок: (10-2)+5 и 10-(2+5).
§ Расставь скобки так, чтобы равенство было верным: 7+3*2=20.
§ Расставь знаки действий и скобки так, чтобы равенства были верными:
5 5 5 5=0, 5 5 5 5=1, 5 5 5 5=2, 5 5 5 5=3, 5 5 5 5=4, 5 5 5 5=5 и т.д.
Методика работы с тождественными преобразованиями выражений:
Тождественные преобразования – это замена одного выражения другим, равным по значению данному.
Так, например, при изучении правила вычитания из числа суммы, учитель показывает детям, как по-разному можно вычесть сумму: 15-7, 15-(5+2), (15-5)-2. При всех преобразованиях значение выражения не меняется – эта особенность и лежит в основе тождественных преобразований выражений. Рассматриваются также свойства и правила:
§ Переместительное свойство сложения 3+8=8+3 (удобнее к большему числу прибавить меньшее).
§ Сочетательное свойство сложения 35+2=(30+5)+2=30+(5+2).
§ Правило вычитания из суммы числа 50-7=(40+10)-7=40+(10-7).
§ Конкретный смысл умножения (до изучения таблицы умножения) 21*3=21+21+21.
§ Переместительное свойство умножения 3*18=18*3 (удобнее большее число умножить на меньшее число).
§ Сочетательное свойство умножение 30*2=(3*10)*2=(3*2)*10.
§ Умножение суммы на число 23*2=(20+3)*2=20*2+3*2.
§ Правило деления суммы на число 65:5=(50+15):5=50:5+15:5.
§ Правило деления произведения на число 560:7=(56*10):7=(56:7)*10.
§ Правило деления числа на произведение 560:70=560:(7*10)=(560:10):7.