ВЕКТОРНАЯ ДИАГРАММА ТРАНСФОРМАТОРОВ

ЭКВИВАЛЕНТНАЯ СХЕМА ТРАНСФОРМАТОРА

Одним из методических приемов, облегчающих исследование электромагнитных процессов и расчет трансформаторов, является замена реального трансформатора с магнитными связями между обмотками эквивалентной электрической схемой (рис. 4.6.1).

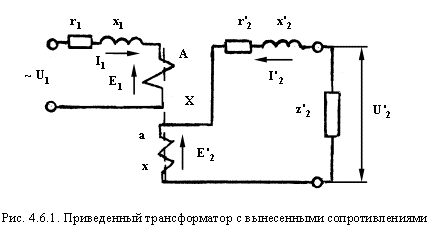
На этом рисунке представлена эквивалентная схема приведенного трансформатора, на которой сопротивления г и х условно вынесены из соответствующих обмоток и включены с ними последовательно. Т.к. k = 1, то E₁ = E₂. Поэтому точки А и а, а также Х и х на приведенном трансформаторе имеют одинаковые потенциалы, что позволит электрически соединить эти точки, получив Т-образную эквивалентную схему замещения (рис. 4.6.2).

Произведя математическое описание этой схемы методами Кирхгофа, можно сделать вывод о том, что она полностью соответствует уравнениям ЭДС и токов реального трансформатора (см. раздел 4.5). Отсюда появляется возможность электрического моделирования трансформатора на ЭВМ. Проводя исследования относительно нагрузки z₂' (единственного переменного параметра схемы), можно прогнозировать реальные ха-рактеристики трансформатора, начиная от холостого хода (z₂'= ) и кончая коротким замыканием (z₂' = 0).

 

Построение векторной диаграммы удобнее начинать с вектора основного потока Ф. Отложим его по оси абсцисс. Вектор I₁₀ опережает его на угол a . Далее строим векторы ЭДС Е₁ и Е₂', которые отстают от потока Ф на 90°. Для определения угла сдвига фаз между E₂' и I₂' следует знать характер нагрузки. Предположим, она - активно-индуктивная. Тогда I₂' отстает от E2' на угол f₂.
Получилась так называемая заготовка векторной диаграммы (рис. 4.7.1.). Для того чтобы достроить ее, необходимо воспользоваться тремя основными уравнениями приведенного трансформатора.

Воспользуемся вторым основным уравнением:

и произведем сложение векторов.
Для этого к концу вектора E₂' пристроим вектор - j I₂' x₂', а к его концу - вектор - I₂' r₂'. Результирующим вектором U₂' будет вектор, соединяющий начало координат с концом последнего вектора.
Теперь используем третье основное уравнение

из которого видно, что вектор тока I₁ состоит из геометрической суммы векторов I₁₀ и - I₂'. Произведем это суммирование и достроим векторную диаграмму.
Теперь вернемся к первому основному уравнению:

Чтобы построить вектор - Е₁ , нужно взять вектор +Е₁ и направить его в противоположную сторону.
Теперь можно складывать с ним и другие векторы: + j I₁ x₁ и I₁ r₁ . Первый будет идти перпендикулярно току, а второй - параллельно ему. В результате получим суммарный вектор u₁.
Построенная векторная диаграмма имеет общий характер. По этой же методике можно осуществить ее построение как для различных режимов, так и для разных характеров нагрузки.