Границы применимости закона Дарси

Коэффициент фильтрации, имеет размерность скорости и характеризует скорость потока через единицу площади сечения, перпендикулярного потоку, под действием единичного градиента напора.

При исследовании фильтрации газа, нефти и их смесей необходимо разделить влияние свойств пористой среды и флюида. Поэтому для разделения свойств флюида и пористой среды равенство (6) представляют в виде:

(8)

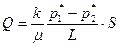или (9)

где μ – динамический коэффициент вязкости,

- приведенное давление,

k – коэффициент проницаемости, который не зависит от свойств жидкости и является динамической характеристикой только пористой среды, м². Проницаемость крупнозернистых песчаников 10^-12 – 10^-13 м² (1 – 0,1 мкм²), проницаемость плотных песчаников 10^-14 м² (0,01 мкм²). Из-за малости этих величин в нефтепромысловой практике получила размерность 1 Д (Дарси) = 1,02·10^-12 м².

Коэффициент фильтрации и проницаемости определяются экспериментально (рис. 1.4) и могут быть связаны между собой соотношением:

(10)

Равенства (8, 9) справедливы, если фильтрационные свойства недеформируемой пористой среды изотропные и однородные, т.е. проницаемость не зависит от направления и постоянна для всех точек.

Из формул (6, 8) имеем или ,

где перепад напора, приходящийся на единицу длины (модуль градиента давления) можно представить в следующем виде

.

Пермеаметр содержит образец исследуемого грунта, общий расход Q фильтрационного потока поддерживается постоянным, напоры Н₁ и Н₂ измеряют двумя пьезометрами, соединенными с пористой средой в сечениях 1 и 2.

Обычно соотношения (6) или (9) называют следствием закона Дарси.

Этот закон является хронологически первым законом теории фильтрации. Закон Дарси можно записать в виде

,

где - коэффициент фильтрации, имеющий размерность скорости;

- гидравлический уклон (или градиент давления).

Закон Дарси связывает меду собой вектор скорости и градиент фильтрационного давления.

Если обе части равенства (9) разделить на площадь сечения, то получим

, (11)

выражение 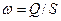имеет размерности скорости, и определяет модуль вектора скорости фильтрации. При определении расхода считается, что вектор скорости фильтрации направлен перпендикулярно плоскости (галерее), через которую фильтруется флюид. Скорость фильтрации – это фиктивная скорость, т.к. она определяется в любой точке сечения пористой среды – и в порах, и в твердом скелете, а на самом деле течение проходит только по поровым каналам с некоторой истинной скоростью υ. Между фиктивной и истинной скоростью существует взаимосвязь:

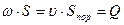или (12)

Таким образом, скорость фильтрации равна истинной средней скорости, умноженной на просветность. Заменять просветность на пористость теоретически неправомерно.

Равенство (11) можно представить в векторной форме. В случае изотропных фильтрационных свойств векторы скорости фильтрации и градиент фильтрационного давления лежат на одной прямой. Поэтому, если умножить равенство (11) на орт , задающий направление фильтрации, получим

(13)

В равенстве (13) множитель 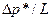представляет собой модуль приведенного давления при линейном законе распределения давления. Тогда можно записать

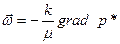(14)

Векторное уравнение (14) представляет собой закон Дарси для изотропной пористой среды.

Знак «минус» в правой части равенства появляется из-за того, что скорость фильтрации направлена в сторону уменьшения приведенного давления. Поэтому векторы скорости фильтрации и градиента фильтрационного давления направлены в разные стороны (градиент давления направлен в сторону роста давления, а скорость фильтрации в обратную сторону – от большего давления к меньшему).

Равенство (14) задает закон Дарси в универсальной безындексной форме записи, справедливой для любой системы координат. В декартовой системе координат равенство записывается в виде

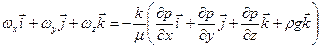, (15)

где - орты декартовой системы координат (ось z направлена вертикально вверх).

Это равенство можно спроектировать на оси координат

, , . (16)

Таким образом, закон Дарси заключается в том, что скорость фильтрации пропорциональна градиенту давления.

Закон Дарси имеет силу, если соблюдаются следующие условия:

1) мелкозернистая пористая среда или достаточно узкие поровые каналы;

2) малая скорость фильтрации при небольшом градиенте давления;

3) незначительные изменения скорости фильтрации или градиента давления.

Закон Дарси справедливдля медленных фильтрационных движений, для которых силы инерции несущественны. Поэтому для таких движений несущественна плотность жидкости, определяющая свойство ее инерции.

Закон Дарси, в дифференциальной форме он имеет вид:

, (17)

где 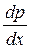- градиент давления (сил трения), ω – скорость фильтрации, m - коэффициент динамической вязкости, k – коэффициент проницаемости.

Знак (-) в левой части формулы (17) означает, что течение газа происходит в направлении, противоположном росту давления.

Фундаментальный закон фильтрации (17) устанавливает связь между скоростью фильтрации и градиентом давления.

 

1.4. Нелинейные законы фильтрации/ввести нумерацию/

Проведенные в дальнейшем эксперименты показали, что закон Дарси не является универсальным и нарушаются области малых и больших скоростей. Нарушение в области малых скоростей связано с молекулярным эффектом. Причины, вызывающие отклонение от закона Дарси при больших скоростях, являются до настоящего времени предметом дискуссии среди исследователей.

В 1901 году австрийский ученый Форхгейме, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости двучленным законом фильтрации:

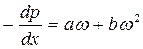, (18)

Двучленный закон фильтрации в дифференциальной форме при прямолинейной фильтрации газа в принятых сейчас обозначениях, без учета силы тяжести имеет два вида записи:

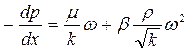, (19)

или

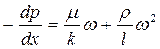(20)

где b - дополнительная константа пористой среды, определяемая экспериментально,

l – коэффициент макрошероховатости, характеризующий структуру порового пространства, r - плотность газа (жидкости).

Первое слагаемое в правой части уравнения (19) учитывает потери давления вследствие вязкости жидкости, второе слагаемое – инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов.

При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации (больших значений числа Рейнольдса). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других физико-химических эффектов и больших поверхностных сил (сил взаимодействия между флюидом и твердым скелетом). При очень малых скоростях фильтрации неньютоновскими свойствами в пористой среде могут обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях исчезает. В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относят аномальные нефти и буровые растворы. Поэтому для качественного изучения вопроса и количественной оценки этих эффектов необходимо отказаться от модели вязкой однородной жидкости и заменить ее какой-либо другой реологической моделью пластового флюида.

Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньтоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом. Для случая одномерного линейного потока его можно представить в виде

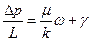, при 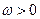, (21)

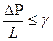, при ,

где - предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента давления фильтрационное течение отсутствует, этот параметр измеряется в лабораторных условиях. зависит от начального сдвига жидкости и эффективного диаметра капилляра.

Закон фильтрации записывают также в виде одночленной степенной формулы:

(22)

где С и n - постоянные, определяемые опытным путем, причем 1< n < 2.

При n = 1 из (22) получается закон Дарси, при n = 2 – квадратичный закон А.А. Краснопольского.

Таким образом, формула (19) имеет два параметра b и k, которые подлежат дальнейшему изучению и установлению связи между ними.

Входящий в линейный закон фильтрации Дарси (17) коэффициент проницаемости определяется при исследовании кернов или на основе гидродинамических исследований.

Исследованиями показано, что для пористых сред коэффициент проницаемости зависти от размера зерен и их дисперсности, коэффициента пористости, формы зерен, степени их сцементированности и. т. д.

Л.С. Лейбензон предложил выразить коэффициент проницаемости в виде:

(23)

где d – линейный размер (диаметр) зерен пористой среды, Sl – безразмерный критерий (число Слихтера), зависящий от коэффициента пористости и структуры порового пространства, т. е.

(24)

где e - некоторый параметр, характеризующий структуру порового пространства пласта, m – коэффициент пористости.

 

В связи с тем, что линейный закон фильтрации Дарси всё-таки является приближенным законом, при увеличении скорости фильтрации жидкости и соответствующем увеличении скоростного напора сделанное ранее при выводе линейного закона фильтрации допущение может оказаться несправедливым, тогда и возникнут погрешности в расчетах. В этих случаях говорят, что линейный закон фильтрации (закон Дарси) имеет верхнюю и нижнюю границы применения.

Верхняя границаопределяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением Re_крчисла Рейнольдса:

, , (25)

где d– линейный размер пористой среды,

v– кинематический коэффициент вязкости флюида.

В таких случаях принято говорить о так называемых нелинейных законах фильтрации, например выражения (18 – 20).

Первая количественная оценка верхней границы применимости закона Дарси была выполнена Павловским, который, опираясь на результаты Слихтера, полученные для модели идеального грунта, и полагая характерный размер dравный эффективному диаметру d_эфвывел следующую формулу для числа Рейнольдса:

, (26)

Использовав эту формулу и данные экспериментов, Н.Н. Павловский установи, что критическое значение числа Рейнольдса находится в пределах

Достаточно узкий диапазон изменения значений Re_кробъясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.

Для удобства обработки результатов многочисленных экспериментов различных авторов В.Н.Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси

. (27)

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Из выражения (17) следует, что если параметр Дарси равен единицы

, (28)

то закон Дарси справедлив.

Таким образом, равенство (28) должно выполняться при Re< Re_кр. Данный параметр упрощает исследование границы применимости линейного закона фильтрации.

Таблица 1.

Интервалы критических значений Reдля различных образцов пористых сред

Образец пористой среды	Диапазон критических значений
Однородная дробь	13-14
Однородный крупнозернистый песок	3-10
Неоднородный мелкозернистый песок с преобладанием фракций диаметром менее 0,1 мм	0,34-0,24
Сцементированный песчаник	0,05-1,4

 

Однако вследствие различной структуры и состава пористых сред получить универсальную зависимость не удается.

Нижняя границаопределяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействия с твердым скелетом пористой среды при достаточно малых скоростях фильтрации (например, выражение 21).

Задачи из Басниева.

 

1. При фильтрации жидкости с постоянным расходом через несцементированную пористую среду произошло вымывание мелких фракций песка. Изменилась ли при этом скорость фильтрации и средняя скорость движения жидкости?

 

2. Куб с ребром 1 м наполнили шарами диаметром 10 см каждый, а куб с ребром 1 см точно так же уложили шарами диаметром 1 мм каждый. Пористость какой засыпки больше?

 

3. Показать, что если образец пористого материала, имеющий объем Vи пористость m, разбить на nчастей объемом V_i(i = 1, …, n), то , где m_i- пористость i-й части. Рассмотреть также случай, когда все V_iодинаковы.

 

4. Определите пористость фиктивного грунта, сложенного шарами диаметром D, центры которых находятся в вершинах кубической решетки с периодом D.

Ответ: 1 – π/6 =0,476.

 

5. Определить удельную поверхность фиктивного грунта, пористость которого m= 0,25 и диаметр шаров 0,2 мм. Найти число шаров в 1 м³.

 

6. Определить пористость, удельную поверхность и просветность для рыхлой кубической упаковки шаров.

 

7. Определить пористость для кубической и гексагональной упаковок шаров.

 

8. Определить коэффициент проницаемости пористой среды (в м² и Дарси), если известно, что коэффициент фильтрации k_ф= 0,3·10 ^{– 4} см/с, кинематический коэффициент вязкости жидкости ν = 10 ^{– 6} м²/с.

 

9. Определить проницаемость при фильтрации через образец площадью 1 см², при перепаде давления 1 кгс/см² с расходом жидкости 1 см³/с, если длина образца 1 см, а фильтрующая жидкость имеет динамический коэффициент вязкости 1 сП (один сантипуаз).

Решение. Из формулы (1.9) .

Переведем все размерности в СИ:

площадь 1 см² = 10 ^{– 4} м², давление 1 кгс/см² = 98 кПА, расход 1 см³/с = 10^-6 м³/с, длина 1 см = 10^-2 м, вязкость 1 сП = 0,01 П (Пуаз) = 0,001 Па·с =1 мПа·с

м² = 1Д (Дарси) ≈ 1 мкм².

10. Определить коэффициент фильтрации для керна, помещенного под углом α к горизонту, если массовый расход жидкости равен Q_м, плотность жидкости ρ и вязкость μ, разница напоров в начале и конце керна составляет ΔН, площадь сечения S, длина керна L.

 

11. Образец пористой среды длиной 10 см и диаметром 5 см после насыщения под вакуумом керосином с плотностью 810 кг/м³ стал тяжелее на 20 г. Определить коэффициент пористости образца.

 

 

Щелкачев стр. 80

Оценить влияние размеров поверхностей поровых каналов на величину сил сопротивления, определить суммарную поверхность песчинок, заключенных в 1 м³ песчаного пласта. Примем форму песчинок шарообразной, диаметр их одинаковым и обозначим: N - число песчинок в 1 м³ пласта; r- радиус песчинки; поверхность песчинки ; объем песчинки /в формуле ω/ ; пористость пласта m.

Тогда, V₁ – весь объем шаров,V₂– объем породы.

Суммарная поверхность Sпесчинок, заключенных в 1 м³ песчаного пласта, равна:

 

σ – нет расшиф.