Аналитический метод определения передаточных отношений. Предельные передаточные отношения элементов кинематической цепи.
Предельные передаточные отношения элементов кинематической цепи.
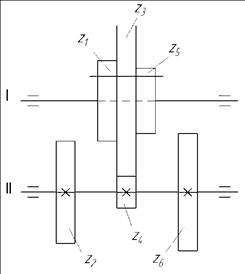
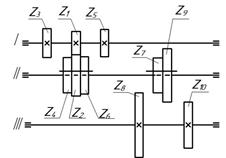
Для несложных коробок скоростей расчет проще производить аналитическим методом, сущность которого рассмотрим на примере коробки скоростей, изображенной на рисуноке 2.1.
Число оборотов шпинделя (вала III) при различных положениях, блоков z4 —z2 —z6 и z7— z9 будет

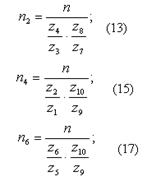
Число оборотов n входного вала I принимается равным
n = nmахφx,
где nmax- верхний предел регулирования;
φ - знаменатель ряда;
х - целое число, может быть положительным, отрицательным и равным нулю.
Примем для простоты х=0, тогда для нашего случая
n = n6.
Учитывая это, из зависимости (17) имеем
 .
.
На этом основании можем принять

Из зависимости (16) следует

Имея в виду, что , получим .


Таким же образом при решении зависимости (15)определим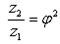 ,
,
и, наконец, из зависимости (14) следует .

В итоге передаточные числа зубчатых колес для рассмотренном схемы будут иметь следующие значения:

В общем случае, когда х не равно нулю (х ≠ 0),

Здесь а и b показатели степени, причем а + b = х. Анализ полученных зависимостей показывает, что для получения геометрического ряда чисел оборотов при одновременной стандартизации числа зубьев в различных коробках с одним и тем же φ желательно, чтобы передаточные числа отдельных пар зубчатых колес были выражены через знаменатель ряда φ
Предельные передаточные отношения элементов кинематической цепи
Воизбежание больших размеров колес а следовательно больших размеров КС и КП. Практикой установлен следующие ограничения на передаточные отношения.
· для КС с прямозубыми колесами предаточное отношение От 1.4 -до 2.0
· для КС с косозубыми колесами передаточное отношение от 1.5 до 2.0
11. Последовательность кинематического расчёта коробок скоростей и коробок подач.
12. Графоаналитический метод кинематического расчёта.
Метод заключается в графическом изображении структурной сетки, и далее построении графика частот вращения.