Выведение итогов
| Регрессионная статистика | ||||||
| Множественный R | 0,806634 | |||||
| R-квадрат | 0,650659 | |||||
| Нормированный R-квадрат | 0,585157 | |||||
| Стандартная ошибка | 0,073662 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| Показатель | df | SS | MS | F | ||
| Регрессия | 0,161702 | 0,053900 | 9,933511 | |||
| Остаток | 0,086818 | 0,005426 | ||||
| Итого | 0,248520 | |||||
| Показатель | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | ||
| Y-пересечение | -0,199947 | 0,451283 | -0,443064 | 0,663651 | ||
| Переменная X 1 | -0,002977 | 0,001269 | -2,345899 | 0,032196 | ||
| Переменная X 2 | 0,013347 | 0,002845 | 4,691053 | 0,000245 | ||
| Переменная X3 | 0,015308 | 0,036151 | 0,423457 | 0,677599 | ||
Модель зависимости объема реализации продукции от всех факторов имеет вид
У= -0,200-0,003х1 + 0,013х2+ 0,015х3
Проверку значимости уравнения регрессии проводим на основе F-критерия Фишера. Расчетное значение =9,93> табличного 3,24 (при числе степеней свободы 3 и 16) и, следовательно, построенное уравнение регрессии значимо.
Множественный коэффициент корреляции R=0.807 свидетельствует о тесной связи между признаками.
Множественный коэффициент детерминации R2=0,651 говорит о том, что объем реализации продукции на 65% зависит от включенных факторов и на 35% от других факторов, не включенных в модель.
Расчетные значения Стьюдента равны tа1=-2.35 ; tа2=4,69 tа3=0,42. табличное значение критерия при уровне значимости 0,05 и числе степеней свободы (n-k-1)=16 равно 2,12. Следовательно, выполняются неравенства |tрасч| > tтабл для а1 и а2, а коэффициент а3 незначим и из модели нужно исключить.
На втором шаге построим модель зависимости объема реализации продукции от цены продукции и расходов на рекламу.
1. Для проведения корреляционного анализа воспользуемся программой «Анализ данных», инструмент «Корреляция»
В результате получаем
| У | Х1 | Х2 | |
| У | |||
| Х1 | -0,30497 | ||
| Х2 | 0,727375 | 0,051692 |
Анализ полученных коэффициентов парной корреляции показывает, что слабая связь между У и Х1
Коэффициент множественной корреляции
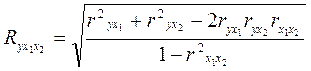
| № организации | Объем реализации продукции, млн руб (У) | Расходы на рекламу, тыс. руб. (Х1) | Цена единицы продукции, руб. (Х2) |
| 1,27 | |||
| 1,34 | |||
| 1,25 | |||
| 1,28 | |||
| 1,43 | |||
| 1,25 | |||
| 1,53 | |||
| 1,57 | |||
| 1,27 | |||
| 1,46 | |||
| 1,28 | |||
| 1,55 | |||
| 1,35 | |||
| 1,49 | |||
| 1,46 | |||
| 1,25 | |||
| 1,29 | |||
| 1,28 | |||
| 1,33 | |||
| 1,51 |
2. Построим модель зависимости. Воспользуемся программой «Анализ данных», инструмент «Регрессия»
Модель зависимости объема реализации продукции от цены продукции и расходов на рекламу имеет вид
У= -0,264-0,003х1 + 0,014х2