Если матрица нулевая, то стоп, граф ациклический, иначе матрица содержит вершины, входящие в циклы
F
J
А, 1 В, 1
Рис. 4.14. Построение кодовой таблицы
Тогда для строки S будет получен следующий код
S=11011110101000000
Длина кода составляет 17 бит, что меньше по сравнению с укороченным кодом.
Теперь рассмотрим процесс декодирования. Алгоритм распаковки кода можно сформулировать следующим образом.
Распаковка
1. i:=0, j:=0;
2. если i>n, то стоп строка распакована, иначе i:=i+1;
3. node:= root;
4. если b(i)=0, то node:=left(node), иначе node:=right(node)
5. если left(node)=0 и right(node)=0, то j:=j+1, s(j):= str(node), перейти к шагу 2, иначе i:=i+1, перейти к шагу 4
В алгоритме корень дерева обозначен как root, а Left(node) и right(node) обозначают левый и правый потомки узла node.
D
C
A B
i
код строки b 110111
строка s А В С
Рис. 4.15. Процесс распаковки кода
На практике такие способы упаковки используются не только для текстов, но и для произвольных двоичных данных. Дело в том, что любой файл можно рассматривать как последовательность байт. Тогда дерево кодирования можно построить не для символов, а для значений байт, встречающихся в кодируемом файле. Поскольку байт может принимать 256 значений, то соответствующее дерево будет иметь не более 256 листьев. В узлах дерева после его полного построения нет необходимости хранить несколько значений кодов и частоты повторения. Для кодирования и декодирования достаточно хранить только одно значение кода и только для листового узла. Поэтому такой способ представления кодовой таблицы является достаточно компактным.
Схемы кодирования подобного типа используются в программах архивации данных и сжатия растровых изображений в форматах графических файлов.
4.4.4. Представление выражений с помощью деревьев
С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу – операция. В общем случае дерево при этом может оказаться не бинарным.
Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным.
* - ( A + B ) * ( (C+cos( D + E )-f (a, b, c, d, e) )
- х -
+ + f
А В С cos a b c d e
+
d e
Рис.4.16. Представление арифметического выражения произвольного вида в виде дерева.
f ( a + b, sin c )
+ sin
a b c
Рис. 4.17. Представление арифметического выражения в виде бинарного дерева
Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.
Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения.
Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным
Пример: (1+10)*5
1) *
+ 5
1 10
2) *
11 5
3) 55
Рис.4.18. Вычисление арифметического выражения с помощью бинарного дерева
((aVb)&(cVd))&(e&fVa&b)
&
& V
V V & &
a b c d e f a b
Рис. 4.19. Представление логического выражения в виде бинарного дерева
4.5. Представление сильноветвящихся деревьев
До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья. Каждый элемент для представления бинарного дерева должен содержать как минимум три поля – значение или имя узла, указатель левого поддерева, указатель правого поддерева. Произвольные деревья могут быть бинарными или сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно.
Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев.
Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов.
a
b c d e
f g h
 |
a b c d e f g h
nil a a a a b b b
b f nil nil nil nil nil nil
nil c d e nil g h nil
элемент
список потомков элемент дерева
следующий
Рис.4.20. Представление сильноветвящихся деревьев в виде списков
4.6. Применение сильноветвящихся деревьев
Один из примеров применения сильноветвящихся деревьев был связан с представлением арифметических выражений произвольного вида. Рассмотрим использование таких деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет собой одно или несколько сильноветвящихся деревьев. В файловой системе MS Dos корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью - непустым каталогам.
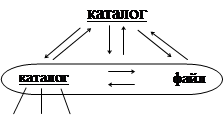
один уровень
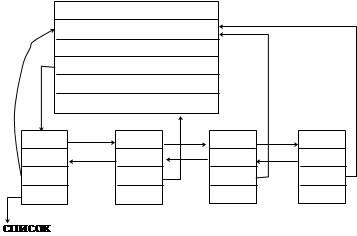имя каталога/файла
тип (каталог или файл)
up
down ¯
last ß
next à
next next next nil
nil last last last
up up up up
down nil nil nil
Рис.4.21. Представление логической структуры каталогов и файлов в виде сильноветвящегося дерева.
Для представления такой структуры используем расширение спискового представления сильноветвящихся деревьев. Способы представления деревьев, рассмотренные ранее, являются предельно экономичными, но не очень удобными для перемещения по дереву в разных направлениях. Именно такая задача встает при просмотре структуры каталогов. Необходимо осуществлять “навигацию” – перемещаться из текущего каталога в каталог верхнего или нижнего уровня, или от файла к файлу в пределах одного каталога.
Для облегчения этой задачи сделаем списки потомков двунаправленными. Для этого достаточно ввести дополнительный указатель на предыдущий узел ”last”. С целью упрощения перемещения по дереву от листьев к корню введем дополнительный указатель на предок текущего узла “up”. Общими с традиционными способами представления являются указатели на список потомков узла “down” и следующий узел “next”.
Для представления оглавления диска служат поля имя и тип файла/каталога. Рассмотрим программу, которая осуществляет чтение структуры заданного каталога или диска, позволяет осуществлять навигацию и подсчет места занимаемого любым каталогом.
program dir_tree;
uses dos;
type node=record
name: string[50]; {Имя каталога/файла}
size: longint; {Размер файла (байт) }
node_type: char; {Тип узла (файл –'f' / каталог-'c')}
up,down: pointer; {Указатели на предка и список потомков}
last,next: pointer; {Указатели на соседние узлы}
end;
var
n,i,l:integer;
root, current_root: pointer;
pnt, current:^node;
s : searchrec;
str: string;
procedure create_tree(local_root:pointer);
{Отображение физического оглавления диска в логическую структуру}
var
local_node, local_r_node, local_last : ^node;
procedure new_node;
{Создание нового узла в дереве каталогов и файлов}
begin
new(local_node);
local_node^.last:=local_last;
if not(local_last=nil) then local_last^.next:=local_node;
local_node^.next:=nil;
local_node^.down:=nil;
local_node^.up:=local_r_node;
if local_r_node^.down =nil then local_r_node^.down:=local_node;
local_node^.name:=local_r_node^.name+'\'+s.name;
if s.attr and Directory = 0 then local_node^.node_type:='f'
else local_node^.node_type:='c';
local_node^.size:=s.size;
local_last:=local_node;
end;
begin
local_r_node:=local_root;
local_last:=nil;
findfirst(local_r_node^.name+'\*.*',anyfile,s);
if doserror = 0 then
begin
if (s.name<>'.') and (s.name<>'..') and (s.attr and VolumeID = 0)
then new_node;
while doserror=0 do begin
findnext(s);
if (doserror = 0) and (s.name<>'.') and (s.name<>'..')
and (s.attr and VolumeID = 0)
then new_node;
end
end;
if not (local_r_node^.down=nil) then
begin
local_node:=local_r_node^.down;
repeat
if local_node^.node_type='c' then create_tree(local_node);
local_node:=local_node^.next
until local_node=nil
end
end;
procedure current_list;
{Вывод оглавления текущего каталога}
begin
current:=current_root;
writeln('текущий каталог - ', current^.name);
if current^.node_type='c'then
begin
pnt:=current^.down;
i:=1;
repeat
writeln (i:4,'-',pnt^.name);
pnt:=pnt^.next;
i:=i+1
until pnt=nil
end;
end;
procedure down;
{Навигация в дереве каталогов. Перемещение на один уровень вниз}
begin
current:=current_root;
if not (current^.down=nil) then
begin
current:= current^.down;
writeln('номер в оглавлении'); readln; read(l);
i:=1;
while (i<l) and not (current^.next=nil) do
begin
current:=current^.next;
i:=i+1
end;
if (current^.node_type='c') and not (current^.down=nil)
then current_root:= current;
end;
end;
procedure up;
{Навигация в дереве каталогов. Перемещение на один уровень вверх}
begin
current:=current_root;
if not (current^.up=nil) then current_root:=current^.up;
end;
procedure count;
{Расчет числа файлов и подкаталогов иерархической структуры каталога}
var
n_files, n_cats :integer;
procedure count_in (local_root : pointer);
var
local_node, local_r_node: ^node;
begin
local_r_node:=local_root;
if not (local_r_node^.down=nil) then
begin
local_node:=local_r_node^.down;
repeat
if local_node^.node_type='f' then n_files:=n_files+1
else
begin
n_cats:=n_cats+1;
count_in (local_node)
end;
local_node:=local_node^.next
until local_node=nil
end
end;
begin
n_files:=0; n_cats:=0;
count_in (current_root);
writeln ('файлы : ',n_files, ' каталоги: ', n_cats);
end;
procedure count_mem;
{Расчет физического объема иерархической структуры каталога}
var
mem :longint;
procedure count_m_in (local_root : pointer);
var
local_node, local_r_node: ^node;
begin
local_r_node:=local_root;
if not (local_r_node^.down=nil) then
begin
local_node:=local_r_node^.down;
repeat
if local_node^.node_type='f' then
mem:=mem+local_node^.size
else
count_m_in (local_node);
local_node:=local_node^.next
until local_node=nil
end
end;
begin
mem:=0;
count_m_in (current_root);
writeln ('mem ', mem, ' bytes');
end;
{----------основная программа----------}
begin
new(current);
{Инициализация корня дерева каталогов и указателей для навигации}
root:=current; current_root:=current;
writeln('каталог ?'); read(str); writeln(str);
current^.name:=str;
current^.last:=nil; current^.next:=nil;
current^.up:=nil; current^.down:=nil;
current^.node_type:='c';
{Создание дерева каталогов}
create_tree(current);
if current^.down=nil then current^.node_type:=' ';
repeat
{ Интерактивная навигация }
writeln ('1-список');
writeln('2-вниз');
writeln('3-вверх');
writeln('4-число файлов');
writeln('5-объем');
readln(n);
if n=1 then current_list;
if n=2 then down;
if n=3 then up;
if n=4 then count;
if n=5 then count_mem;
until n=0
end.
Для чтения оглавления диска в данной программе используются стандартные процедуры findfirst и findnext, которые возвращают сведения о первом и последующих элементах в оглавлении текущего каталога.
В процессе чтения корневого каталога строится первый уровень потомков в списковой структуре дерева. Далее процедура построения поддерева вызывается для каждого узла в корневом каталоге. Затем процесс повторяется для всех непустых какталогов до тех пор, пока не будет построена полная структура оглавления.
Все операции по просмотру содержимого каталогов и подсчету занимаемого объема производятся не с физическими каталогами и файлами, а с созданным динамическим списковым представлением их логической структуры в виде сильноветвящегося дерева.
В данном примере программы для каждого файла или каталога хранится его полное имя в MS-DOS, которое включает имя диска и путь. Если программу несколько усложнить, то можно добиться более эффективного использования динамической памяти. Для этого потребуется хранить в узле дерева только имя каталога или файла, а полое имя – вычислять при помощи цепочки имен каталогов до корневого узла.
4.7. Представление графов
Граф можно представить в виде списочной структуры, состоящей из списков двух типов – списка вершин и списков ребер. Элемент списка вершин содержит поле данных и два указателя. Один указатель связывает данный элемент с элементом другой вершины. Другой указатель связывает элемент списка вершин со списком ребер, связанных с данной вершиной. Для ориентированного графа используют список дуг, исходящих из вершины. Элемент списка дуг состоит только из двух указателей. Первый указатель используется для того, чтобы показать в какую вершину дуга входит, а второй – для связи элементов в списке дуг вершины.
a b
c d
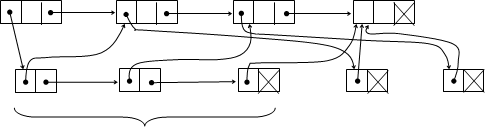
A B C D
(a,b) (a,c) (a,d) (b,d) (c,d)
список дуг, связанных с вершиной a
элементы списка дуг
Рис. 4.22. Представление графа в виде списочной структуры
Очень распространенным является матричный способ представления графов. Для представления ненаправленных графов обычно используют матрицы смежности, а для ориентированных графов – матрицы инцидентности. Обе матрицы имеют размерность n*n, где n-число вершин в графе. Вершины графа последовательно нумеруются.
Матрица смежности имеет значение ноль в позиции m (i,j), если не существует ребра, связывающего вершину i с вершиной j, или имеет единичное значение в позиции m (i,j), если такое ребро существует.
Правила построения матрицы инцидентности аналогичны правилам построения матрицы инцидентности. Разница состоит в том, что единица в позиции m (i,j) означает выход дуги из вершины i и вход дуги в вершину j.
b c e
a d
Матрица смежности
a b c d e
a 0 0 1 1 0
b 0 0 1 0 0
c 0 1 0 1 1
d 1 0 1 0 1
e 1 0 1 1 0
Матрица инцидентности
a b c d e
a 0 0 1 1 0
b 0 0 1 0 0
c 0 0 0 1 1
d 0 0 0 0 1
e 0 0 0 1 0
Рис.4.23. Матричное представление графа
Поскольку матрица смежности симметрична относительно главной диагонали, то можно хранить и обрабатывать только часть матрицы. Можно заметить, что для хранения одного элемента матрицы достаточно выделить всего один бит.
4.8. Алгоритмы на графах
В некоторых матричных алгоритмах обработки графов используются так называемые матрицы путей. Определим понятие пути в ориентированном графе. Под путем длиной k из вершины i в вершину j мы будем понимать возможность попасть из вершины i в вершину j за k переходов, каждому из которых соответствует одна дуга. Одна матрица путей m k содержит сведения о наличии всех путей одной длины k в графе. Единичное значение в позиции (i,j) означает наличие пути длины k из вершины i в вершину j.
b c e
a d
m 1
a b c d e
a 0 0 1 1 0
b 0 0 1 0 0
c 0 0 0 1 1
d 0 0 0 0 1
e 0 0 0 1 0
m 2
a b c d e
a 0 0 0 1 1
b 0 0 0 1 1
c 0 0 0 1 1
d 0 0 0 1 0
e 0 0 0 0 1
m 3
a b c d e
a 0 0 0 1 1
b 0 0 0 1 1
c 0 0 0 1 1
d 0 0 0 0 1
e 0 0 0 1 0
Рис.4.24. Матрицы путей
Матрица m1 полностью совпадает с матрицей инцидентности. По матрице m 1 можно построить m 2 . По матрице m 2 можно построить m 3 и т. д. Если граф является ациклическим, то число мариц путей ограничено. В противном случае матрицы будут повторяться до бесконечности с некоторым периодом, связанным с длиной циклов. Матрицы путей не имеет смысла вычислять до бесконечности. Достаточно остановиться в случае повторения матриц.
Если выполнить логическое сложение всех матриц путей, то получится транзитивное замыкание графа.
M tr = m 1 OR m 2 OR m 3 …
В результате матрица будет содержать все возможные пути в графе.
 | |||
 |
b c e b c e
a d a d
m tr
a b c d e
a 0 0 1 1 1
b 0 0 1 1 1
c 0 0 0 1 1
d 0 0 0 1 1
e 0 0 0 1 1
Рис. 4.25. Транзитивное замыкание в графе
Наличие циклов в графе можно определить с помощью эффективного алгоритма. Алгоритм может быть реализован как для матричного, так и для спискового способа представления графа.
Принцип выделения циклов следующий. Если вершина имеет только входные или только выходные дуги, то она явно не входит ни в один цикл. Можно удалить все такие вершины из графа вместе со связанными с ними дугами. В результате появятся новые вершины, имеющие только входные или выходные дуги. Они также удаляются. Итерации повторяются до тех пор, пока граф не перестанет изменяться. Отсутствие изменений свидетельствует об отсутствии циклов, если все вершины были удалены. Все оставшиеся вершины обязательно принадлежат циклам.
Сформулируем алгоритм в матричном виде
1. Для iот 1 до n выполнить шаги 1-2
2. Если строка M(i ,*) = 0, то обнулить столбец i
3. Если столбец M(*, i) = 0, то обнулить строку i
4. Если матрица изменилась, то выполнить шаг 1
a d
b c e
f
начало a b c d e f
итерация 1 b c d e f
итерация 2 c d e f
итерация 3 c d e
итерация 4 d e
итерация 5 d e
итерация 1
a b c d e f
a 0 0 0 0 0 0 < обнуляемая строка
b 1 0 0 0 0 0
c 0 0 0 1 1 1 < обнуляемая строка
d 0 0 0 0 1 0
e 0 0 0 1 0 0
f 0 1 0 0 0 0
Рис. 4.26. Поиск циклов в графе
Достоинством данного алгоритма является то, что происходит одновременное определение цикличности или ацикличности графа и формирование списка вершин, входящих в циклы. В матричной реализации после завершения алгоритма остается матрица инцидентности, соответствующая подграфу, содержащему все циклы исходного графа.
ЛИТЕРАТУРА
1. Вирт Н. Алгоритмы и структуры данных. – М: Мир, 1989 –360с.
2. Сибуя М., Ямамото Т. Алгоритмы обработки данных. – М: Мир, 1986 –218с.
3. Лэгсам Й, Огенстайн М. Структуры данных для персональных ЭВМ – М: Мир, 1989 –586с.
4. Турбо Паскаль 7.0 – Киев: BHV, 1998 – 448c.
СОДЕРЖАНИЕ
1. Основные структуры данных............................................................................................. 3
1.1. Массивы............................................................................................................................. 3
1.2. Записи................................................................................................................................. 4
1.3. Множества.......................................................................................................................... 6
1.4. Динамические структуры данных................................................................................... 6
1.4.1. Линейные списки........................................................................................................... 7
1.4.2. Циклические списки.................................................................................................... 13
1.4.3. Мультисписки............................................................................................................... 16
1.5. Представление стека и очередей в виде списков........................................................ 18
1.5.1. Стек................................................................................................................................ 18
1.5.2. Очереди......................................................................................................................... 19
2. Задачи поиска в структурах данных................................................................................ 22
2.1. Линейный поиск............................................................................................................. 22
2.2. Поиск делением пополам (двоичный поиск)............................................................... 23
2.3. Поиск в таблице.............................................................................................................. 26
2.3.1. Прямой поиск строки................................................................................................... 27
2.3.2. Алгоритм Кнута, Мориса и Пратта............................................................................ 29
2.3.3. Алгоритм Боуера и Мура............................................................................................. 32
3. Методы ускорения доступа к данным.............................................................................. 34
3.1. Хеширование данных..................................................................................................... 34
3.1.1. Методы разрешения коллизий.................................................................................... 35
3.1.2. Переполнение таблицы и рехеширование................................................................ 40
3.1.3. Оценка качества хеш-функции................................................................................... 43
3.2. Организация данных для ускорения поиска по вторичным ключам........................ 45
3.2.1. Инвертированные индексы......................................................................................... 46
3.2.2. Битовые карты.............................................................................................................. 47
4. Представление графов и деревьев.................................................................................... 48
4.1. Бинарные деревья............................................................................................................ 49
4.2. Представление бинарных деревьев............................................................................... 50
4.3. Прохождение бинарных деревьев................................................................................. 55
4.4. Алгоритмы на деревьях.................................................................................................. 58
4.4.1. Сортировка с прохождением бинарного дерева....................................................... 58
4.4.2. Сортировка методом турнира с выбыванием........................................................... 59
4.4.3. Применение бинарных деревьев для сжатия информации..................................... 62
4.4.4. Представление выражений с помощью деревьев..................................................... 64
4.5. Представление сильноветвящихся деревьев................................................................ 67
4.6. Применение сильноветвящихся деревьев.................................................................... 68
4.7. Представление графов.................................................................................................... 74
4.8. Алгоритмы на графах..................................................................................................... 75
ЛИТЕРАТУРА........................................................................................................................ 79