D, 5 ABC, 5
D 11
20 0,1,3,4,5,8,10,20
. . .
30, 1, 3
0 0
A C
C D
A C
C D
Поиск
Удаление
Вставка
1. i = 0
2. a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
3. Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
4. i = i + 1, перейти к шагу 2
5. a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
Рассматривая возможность выхода за пределы адресного пространства таблицы, мы не учитывали факторы заполненности таблицы и удачного выбора хеш-функции. При большой заполненности таблицы возникают частые коллизии и циклические переходы в начало таблицы. При неудачном выборе хеш-функции происходят аналогичные явления. В наихудшем варианте при полном заполнении таблицы алгоритмы циклического поиска свободного места приведут к зацикливанию. Поэтому при использовании хеш-таблиц необходимо стараться избегать очень плотного заполнения таблиц. Обычно длину таблицы выбирают из расчета двукратного превышения предполагаемого максимального числа записей. Не всегда при организации хеширования можно правильно оценить требуемую длину таблицы, поэтому в случае большой заполненности таблицы может понадобиться рехеширование. В этом случае увеличивают длину таблицы, изменяют хеш-функцию и переупорядочивают данные.
Производить отдельную оценку плотности заполнения таблицы после каждой операции вставки нецелесообразно, поэтому можно производить такую оценку косвенным образом – по числу коллизий во время одной вставки. Достаточно определить некоторый порог числа коллизий, при превышении которого следует произвести рехеширование. Кроме того, такая проверка гарантирует невозможность зацикливания алгоритма в случае повторного просмотра элементов таблицы.
Рассмотрим алгоритм вставки, реализующий предлагаемый подход.
Вставка
1. i = 0
2. a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
3. Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
4. Если i > m , то стоп требуется рехеширование
5. i = i + 1, перейти к шагу 2
В данном алгоритме номер итерации сравнивается с пороговым числом m. Следует заметить, что алгоритмы вставки, поиска и удаления должны использовать идентичное образование адреса очередной записи.
1. i = 0
2. a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
3. Если t(a) = key, то t(a) =удалено, стоп элемент удален
4. Если t(a) = свободно или i>m, то стоп элемент не найден
5. i = i + 1, перейти к шагу 2
1. i = 0
2. a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
3. Если t(a) = key, то стоп элемент найден
4. Если t(a) = свободно или i>m, то стоп элемент не найден
5. i = i + 1, перейти к шагу 2
3.1.3. Оценка качества хеш-функции
Как уже было отмечено, очень важен правильный выбор хеш-функции. При удачном построении хеш-функции таблица заполняется более равномерно, уменьшается число коллизий и уменьшается время выполнения операций поиска, вставки и удаления. Для того чтобы предварительно оценить качество хеш-функции можно провести имитационное моделирование. Моделирование проводится следующим образом. Формируется целочисленный массив, длина которого совпадает с длиной хеш-таблицы. Случайно генерируется достаточно большое число ключей, для каждого ключа вычисляется хеш-функция. В элементах массива просчитывается число генераций данного адреса. По результатам такого моделирования можно построить график распределения значений хеш-функции. Для получения корректных оценок число генерируемых ключей должно в несколько раз превышать длину таблицы.
 число коллизий
число коллизий
Неудачная хеш-функция
удачная хеш-функция
0 n адрес
Области концентрации коллизий
Рис. 3.6. Распределение коллизий в адресном пространстве таблицы
Если число элементов таблицы достаточно велико, то график строится не для отдельных адресов, а для групп адресов. Например, все адресное пространство разбивается на 100 фрагментов и подсчитывается число попаданий адреса для каждого фрагмента. Большие неравномерности свидетельствуют о высокой вероятности коллизий в отдельных местах таблицы. Разумеется, такая оценка является приближенной, но она позволяет предварительно оценить качество хеш-функции и избежать грубых ошибок при ее построении.
Оценка будет более точной, если генерируемые ключи будут более близки к реальным ключам, используемым при заполнении хеш-таблицы. Для символьных ключей очень важно добиться соответствия генерируемых кодов символов тем кодам символов, которые имеются в реальном ключе. Для этого стоит проанализировать, какие символы могут быть использованы в ключе.
Например, если ключ представляет собой фамилию на русском языке, то будут использованы русские буквы. Причем первый символ может быть большой буквой, а остальные – малыми. Если ключ представляет собой номерной знак автомобиля, то также несложно определить допустимые коды символов в определенных позициях ключа.
Рассмотрим пример генерации ключа из десяти латинских букв, первая из которых является большой, а остальные –малыми.
Пример: ключ – 10 символов, 1-й большая латинская буква
2-10 малые латинские буквы
var i:integer;
s:string[10];
begin
s[1]:=chr(random(90-65)+65);
for i:=2 to 10 do s[i]:=chr(random(122-97)+97);
end
В данном фрагменте используется тот факт, что допустимые коды символов располагаются последовательными непрерывными участками в кодовой таблице. Рассмотрим более общий случай. Допустим, необходимо сгенерировать ключ из m символов с кодами в диапазоне от n1 до n2.
Генерация ключа из m символов c кодами в диапазоне от n1 до n2
(диапазон непрерывный)
for i:=1 to m do str[i]:=chr(random(n2-n1)+n1);
На практике возможны варианты, когда символы в одних позициях ключа могут принадлежать к разным диапазонам кодов, причем между этими диапазонами может существовать разрыв.
Генерация ключа из m символов c кодами
в диапазоне от n1 до n4 (диапазон имеет разрыв от n2 до n3)
 |
n1 n2 n3 n4
for i:=1 to m do
begin
x:=random((n4 - n3) + (n2 – n1));
if x<=(n2 - n1) then str[i]:=chr(x + n1)
else str[i]:=chr(x + n1 + n3 – n2)
end;
Рассмотрим еще один конкретный пример. Допустим известно, что ключ состоит из 7 символов. Из них три первые символа – большие латинские буквы, далее идут две цифры, остальные – малые латинские.
Пример: длина ключа 7 символов
1) 3 большие латинские (коды 65-90)
2) 2 цифры (коды 48-57)
3) 2 малые латинские (коды 97-122)
var
key: string[7];
begin
for i:=1 to 3 do key[i]:=chr(random(90-65)+65);
for i:=4 to 5 do key[i]:=chr(random(57-48)+57);
for i:=6 to 7 do key[i]:=chr(random(122-97)+97);
end;
В рассматриваемых примерах мы исходили из предположения, что хеширование будет реализовано на языке Turbo Pascal, а коды символов соответствуют альтернативной кодировке.
3.2. Организация данных для ускорения поиска по вторичным ключам
До сих пор рассматривались способы поиска в таблице по ключам, позволяющим однозначно идентифицировать запись. Мы будем называть такие ключи первичными ключами. Возможен вариант организации таблицы, при котором отдельный ключ не позволяет однозначно идентифицировать запись. Такая ситуация часто встречается в базах данных. Идентификация записи осуществляется по некоторой совокупности ключей. Ключи, не позволяющие однозначно идентифицировать запись в таблице, называются вторичными ключами.
Даже при наличии первичного ключа, для поиска записи могут быть использованы вторичные. Например, поисковые системы internet часто организованы как наборы записей, соответствующих Web-страницам. В качестве вторичных ключей для поиска выступают ключевые слова, а сама задача поиска сводится к выборке из таблицы некоторого множества записей, содержащих требуемые вторичные ключи.
3.2.1. Инвертированные индексы
Рассмотрим метод организации таблицы с инвертированными индексами. Для таблицы строится отдельный набор данных, содержащий так называемые инвертированные индексы. Вспомогательный набор содержит для каждого значения вторичного ключа отсортированный список адресов записей таблицы, которые содержат данный ключ.
Поиск осуществляется по вспомогательной структуре достаточно быстро, так как фактически отсутствует необходимость обращения к основной структуре данных. Область памяти, используемая для индексов,
является относительно небольшой по сравнению с другими методами организации таблиц.
Таблица
(прямая адресация)




 1 A B C
1 A B C
4 A B
5 A C
Структура инвертированных индексов
(списковая структура)
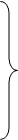 |

A 1 3 4 5
 B 1 4 упорядочена по
B 1 4 упорядочена по
 значению индексов
значению индексов
 C 1 2 3 5
C 1 2 3 5
D 2
Рис.3.7. Метод организации таблицы с инвертированными индексами
Недостатками данной системы являются большие затраты времени на составление вспомогательной структуры данных и ее обновление. Причем эти затраты возрастают с увеличение объема базы данных.
Система инвертированных индексов является чрезвычайно удобной и эффективной при организации поиска в больших таблицах.
3.2.2. Битовые карты
Для таблиц небольшого объема используют организацию вспомогательной структуры данных в виде битовых карт. Для каждого значения вторичного ключа записей основного набора данных записывается последовательность битов. Длина последовательности битов равна числу записей. Каждый бит в битовой карте соответствует одному значению вторичного ключа и одной записи. Единица означает наличие ключа в записи, а ноль –отсутствие.
Таблица
(прямая адресация)




 1 A B C
1 A B C
4 A B
5 A C
битовые карты
1 2 3 4 5
 A 1 0 1 1 1 - массив
A 1 0 1 1 1 - массив

 B 1 0 0 1 0
B 1 0 0 1 0

 битовые строки (длина равна
битовые строки (длина равна
C 1 1 1 0 1 числу элементов таблицы)

D 0 1 0 0 0
Рис.3.8. Организация вспомогательной структуры данных в виде битовых карт
Основным преимуществом такой организации является очень простая и эффективная организация обработки сложных запросов, которые могут объединять значения ключей различными логическими предикатами. В этом случае поиск сводится к выполнению логических операций запроса непосредственно над битовыми строками и интерпретации результирующей битовой строки. Другим преимуществом является простота обновления карты при добавлении записей.
К недостаткам битовых карт следует отнести увеличение длины строки пропорционально длине файла. При этом заполненность карты единицами уменьшается с увеличением длины файла. Для большой длине таблицы и редко встречающихся ключах битовая карта превращается в большую разреженную матрицу, состоящую в основном из одних нулей.
4. Представление графов и деревьев
Теория графов является важной частью вычислительной математики. С помощью этой теории решаются большое количество задач из различных областей. Граф состоит из множества вершин и множества ребер, которые соединяют между собой вершины. С точки зрения теории графов не имеет значения, какой смысл вкладывается в вершины и ребра. Вершинами могут быть населенными пункты, а ребрами дороги, соединяющие их, или вершинами являться подпрограммы, соединенные вершин ребрами означает взаимодействие подпрограмм. Часто имеет значение направления дуги в графе. Если ребро имеет направление, оно называется дугой, а граф с ориентированными ребрами называется орграфом.
Дадим теперь более формально основное определение теории графов. Граф G есть упорядоченная пара (V,E), где V - непустое множество вершин, E - множество пар элементов множества V, пара элементов из V называется ребром. Упорядоченная пара элементов из V называется дугой. Если все пары в Е - упорядочены, то граф называется ориентированным.
Путь - это любая последовательность вершин орграфа такая, что в этой последовательности вершина b может следовать за вершиной a, только если существует дуга, следующая из а в b. Аналогично можно определить путь, состоящий из дуг. Путь начинающийся в одной вершине и заканчивающийся в одной вершине называется циклом. Граф в котором отсутствуют циклы, называется ациклическим.
Важным частным случаем графа является дерево. Деревом называется орграф для которого :
1. Существует узел, в которой не входит не одной дуги. Этот узел называется корнем.
2. В каждую вершину, кроме корня, входит одна дуга.
С точки зрения представления в памяти важно различать два типа деревьев: бинарные и сильноветвящиеся.
В бинарном дереве из каждой вершины выходит не более двух дуг. В сильноветвящемся дереве количество дуг может быть произвольным.
4.1. Бинарные деревья
Бинарные деревья классифицируются по нескольким признакам. Введем понятия степени узла и степени дерева. Степенью узла в дереве называется количество дуг, которое из него выходит. Степень дерева равна максимальной степени узла, входящего в дерево. Исходя из определения степени понятно, что степень узла бинарного дерева не превышает числа два. При этом листьями в дереве являются вершины, имеющие степень ноль.

p1 корень
p2 p3
p6
p4 p5 p1, p2, p3, p4, p5, p6, p7, p8 - узлы
p3, p4, p5, p7, p8 - листья
p7 p8
Рис.4.1. Бинарное дерево
Другим важным признаком структурной классификации бинарных деревьев является строгость бинарного дерева. Строго бинарное дерево состоит только из узлов, имеющих степень два или степень ноль. Нестрого бинарное дерево содержит узлы со степенью равной одному.
а) неполное бинарное дерево б) полное бинарное дерево
 | |||
 | |||
- на всех уровнях
меньше, чем n, узлы имеют
степень 2, на уровне n - 0
Рис.4.2. Полное и неполное бинарные деревья
а) строго бинарное дерево б) не строго бинарное дерево
 |
 - все узлы имеют степень узлов
- все узлы имеют степень узлов
степень 2 или равна 2, 1, 0
степень 0
Рис.4.3. Строго и не строго бинарные деревья
4.2. Представление бинарных деревьев
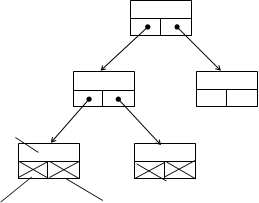
Бинарные деревья достаточно просто могут быть представлены в виде списков или массивов. Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой – с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева.
Можно заметить, что такой способ представления имеет сходство с простыми линейными списками. И это сходство не случайно. На самом деле рассмотренный способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков. Каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.
 p1
p1

p1
p2 p3
p2 p3
имя узла
p4 p5 p4 p5
указатель правого указатель правого
поддерева поддерева
Рис.4.4. Представление бинарного дерева в виде списковой структуры
Приведем пример программы, которая осуществляет создание и редактирование бинарного дерева, представленного в виде списковой структуры
program bin_tree_edit;
type node=record
name: string;
left, right: pointer;
end;
var
n:integer;
pnt_s,current_s,root: pointer;
pnt,current:^node;
s: string;
procedure node_search (pnt_s:pointer; var current_s:pointer);
{Поиск узла по содержимому}
var
pnt_n:^node;
begin
pnt_n:=pnt_s; writeln(pnt_n^.name);
if not not (pnt_n^.name=s) then
begin
if pnt_n^.left <> nil then
node_search (pnt_n^.left,current_s);
if pnt_n^.right <> nil then
node_search (pnt_n^.right,current_s);
end
else current_s:=pnt_n;
end;
procedure node_list (pnt_s:pointer);
{Вывод списка всех узлов дерева}
var
pnt_n:^node;
begin
pnt_n:=pnt_s; writeln(pnt_n^.name);
if pnt_n^.left <> nil then node_list (pnt_n^.left);
if pnt_n^.right <> nil then node_list (pnt_n^.right);
end;
procedure node_dispose (pnt_s:pointer);
{Удаление узла и всех его потомков в дереве}
var
pnt_n:^node;
begin
if pnt_s <> nil then
begin
pnt_n:=pnt_s; writeln(pnt_n^.name);
if pnt_n^.left <> nil then
node_dispose (pnt_n^.left);
if pnt_n^.right <> nil then
node_dispose (pnt_n^.right);
dispose(pnt_n);
end
end;
begin
new(current);root:=current;
current^.name:='root';
current^.left:=nil;
current^.right:=nil;
repeat
writeln('текущий узел -',current^.name);
writeln('1-присвоить имя левому потомоку');
writeln('2-присвоить имя правому потомку');
writeln('3-сделать узел текущим');
writeln('4-вывести список всех узлов');
writeln('5-удалить потомков текущего узла');
read(n);
if n=1 then
begin {Создание левого потомка}
if current^.left= nil then new(pnt)
else pnt:= current^.left;
begin
writeln('left ?');
readln;
read(s);
pnt^.name:=s;
pnt^.left:=nil;
pnt^.right:=nil;
current^.left:= pnt;
end;
end;
if n=2 then
begin {Создание правого потомка}
if current^.right= nil then new(pnt)
else pnt:= current^.right;
begin
writeln('right ?');
readln;
read(s);
pnt^.name:=s;
pnt^.left:=nil;
pnt^.right:=nil;
current^.right:= pnt;
end;
end;
if n=3 then
begin {Поиск узла}
writeln('name ?');
readln;
read(s);
current_s:=nil; pnt_s:=root;
node_search (pnt_s, current_s);
if current_s <> nil then current:=current_s;
end;
if n=4 then
begin {Вывод списка узлов}
pnt_s:=root;
node_list(pnt_s);
end;
if n=5 then
begin {Удаление поддерева}
writeln('l,r ?');
readln;
read(s);
if (s='l') then
begin {Удаление левого поддерева}
pnt_s:=current^.left;
current^.left:=nil;
node_dispose(pnt_s);
end
else
begin {Удаление правого поддерева}
pnt_s:=current^.right;
current^.right:=nil;
node_dispose(pnt_s);
end;
end;
until n=0
end.
В виде массива проще всего представляется полное бинарное дерево, так как оно всегда имеет строго определенное число вершин на каждом уровне. Вершины можно пронумеровать слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве.

 p1 1 р1
p1 1 р1
2 р2 адрес = 2к-1+i-1
p3 3 р3
p2 4 р4
5 р5
6 6
p4 p5 p7 55 7 р7
2n-1
адрес последней
вершины полного дерева
Рис.4.5. Представление бинарного дерева в виде массива
Если число уровней дерева в процессе обработки не будет существенно изменяться, то такой способ представления полного бинарного дерева будет значительно более экономичным, чем любая списковая структура.
Однако далеко не все бинарные деревья являются полными. Для неполных бинарных деревьев применяют следующий способ представления. Бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются. В массив заносятся только те вершины, которые были в исходном неполном дереве. При таком представлении элемент массива выделяется независимо от того, будет ли он содержать узел исходного дерева. Следовательно, необходимо отметить неиспользуемые элементы массива. Это можно сделать занесением специального значения в соответствующие элементы массива. В результате структура дерева переносится в одномерный массив. Адрес любой вершины в массиве вычисляется как
адрес = 2к-1+i-1,
где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков
адрес_L = 2к+2(i-1)
адрес_R = 2к+2(i-1)+1
Главным недостатком рассмотренного способа представления бинарного дерева является то, что структура данных является статической. Размер массива выбирается исходя из максимально возможного количества уровней бинарного дерева. Причем чем менее полным является дерево, тем менее рационально используется память.
4.3. Прохождение бинарных деревьев
В ряде алгоритмов обработки деревьев используется так называемое прохождение дерева. Под прохождением бинарного дерева понимают определенный порядок обхода всех вершин дерева. Различают несколько методов прохождения.
Прямой порядок прохождения бинарного дерева можно определить следующим образом
1. попасть в корень
2. пройти в прямом порядке левое поддерево
3. пройти в прямом порядке правое поддерево

a a b c d e f g h i
b e
c d f g
h i
Рис.4.6. Прямой порядок прохождения бинарного дерева
Прохождение бинарного дерева в обратном порядке можно определить в аналогичной форме
1. пройти в обратном порядке левое поддерево
2. пройти в обратном порядке правое поддерево
3. попасть в корень

a c d b f h i g e a
b e
c d f g
h i
Рис.4.7. Обратный порядок прохождения бинарного дерева
Определим еще один порядок прохождения бинарного дерева, называемый симметричным.
1. пройти в симметричном порядке левое поддерево
2. попасть в корень
3. пройти в симметричном порядке правое поддерево
Порядок обхода бинарного дерева можно хранить непосредственно в структуре данных. Для этого достаточно ввести дополнительное поле указателя в элементе списковой структуры и хранить в нем указатель на вершину, следующую за данной вершиной при обходе дерева.
Представление деревьев в виде массивов также допускает хранение порядка прохождения дерева. Для этого вводится дополнительный массив, в который записываются адрес вершины в основном массиве, следующей за данной вершиной.
 a c b d a f e h g i
a c b d a f e h g i
b e
c d f g
h i

1 a à 6
2 b à 4
3 c à 2
4 d à 1
5 e à 14
6 f à 5
7 g à 15
14 h à 7
15 i
Рис.4.8. Представление симметрично прошитого бинарного дерева в виде массивов
Такие структуры данных получили название прошитых бинарных деревьев. Указатели или адреса, определяющие порядок обхода называют нитями. При этом в соответствии с порядком прохождения вершин
различают право прошитые, лево прошитые и симметрично прошитые бинарные деревья.
4.4. Алгоритмы на деревьях
4.4.1. Сортировка с прохождением бинарного дерева
В качестве примера использования прохождения бинарного дерева можно привести один из способов сортировки. Допустим, мы имеем некоторый массив и пытаемся упорядочить его элементы по возрастанию. Сама сортировка при этом распадается на две фазы
1. построение дерева
2. прохождение дерева
Дерево строится по следующим принципам. В качестве корня создается узел, в который записывается первый элемент массива. Для каждого очередного элемента создается новый лист. Если элемент меньше значения в текущем узле, то для него выбирается левое поддерево, если больше или равен – правое.
Исходный массив:
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

4 15
3 9 14 18
7 9 17 20
5 16
4 5
Прохождение в симметричном порядке:
3, 4, 4, 5, 5, 7, 9, 9, 14, 14, 15, 16, 17, 18, 20
Рис.4.9. Сортировка по возрастанию с прохождением бинарного дерева
Для создания очередного узла происходят сравнения элемента со значениями существующих узлов, начиная с корня.
Во время второй фазы происходит прохождение дерева в симметричном порядке. Результатом сортировки является последовательность значений элементов, извлекаемых их пройденных узлов.
Для того чтобы сделать сортировку по убыванию, необходимо изменить только условия выбора поддерева при создании нового узла во время построения дерева.
4.4.2. Сортировка методом турнира с выбыванием
Приведем другой алгоритм сортировки, основанный на использовании бинарных деревьев. Данный метод получил название турнира с выбыванием. Пусть мы имеем исходный массив
10, 20, 3, 1, 5, 0, 4, 8
Сортировка начинается с создания листьев дерева. В качестве листьев бинарного дерева создаются узлы, в которых записаны значения элементов исходного массива.
Дерево строится от листьев к корню. Для двух соседних узлов строится общий предок, до тех пор, пока не будет создан корень. В узел-предок заносится значение, являющееся наименьшим из значений в узлах-потомках.

1 0
10 1 04
10 20 3 1 5 0 4 8
Рис.4.10. Построение дерева сортировки
В результате построения такого дерева наименьший элемент попадает сразу в корень. Далее начинается извлечение элементов из дерева. Извлекается значение из корня. Данное значение является первым элементом в результирующем массиве. Извлеченное значение помещается в отсортированный массив и заменяется в дереве на специальный символ.
После этого происходит повторное занесение значений в родительские элементы от листьев к корню. При сравнениях специальный символ считается большим по отношению к любому другому значению.
После повторного заполнения из корня извлекается очередной элемент и итерация повторяется. Извлечения элементов продолжаются до тех пор, пока в дереве не останутся одни специальные символы.
 * 0
* 0
1 *
10 1 *4
10 20 3 1 5 * 4 8
Рис.4.11. Замена извлекаемого элемента на специальный символ

1 0, 1
1 4
10 1 5 4
10 20 3 1 5 * 4 8
Рис.4.12. Повторное заполнение дерева сортировки

3 4
10 3 5 4
0 20 3* 5 * 4 8

20 *
20 * * *
* 20 * * * * * *

* 0,1,3,4,5,8,10,20
* *
* * * *
* * * * * * * *
Рис.4.13. Извлечения элементов из дерева сортировки
В результате получим отсортированный массив
0, 1, 3, 4, 5, 8, 10, 20
4.4.3. Применение бинарных деревьев для сжатия информации
Рассмотрим применение деревьев для сжатия информации. Под сжатием мы будем понимать получение более компактного кода.
Рассмотрим следующий пример. Имеется текстовая строка S, состоящая из 10 символов
S = ABCCCDDDDD
При кодировании одного символа одним байтом для строки потребуется 10 байт.
Попробуем сократить требуемую память. Рассмотрим, какие символы действительно требуется кодировать. В данной строке используются всего 4 символа. Поэтому можно использовать укороченный код.
A 00 S = 00, 01, 10, 10, 10, 11, 11, 11, 11, 11 20 бит
B 01
C 10
В данном случае мы проанализировали текст на предмет использования символов. Можно заметить, что различные символы имеют различную частоту повторения. Существуют методы кодирования, позволяющие использовать этот факт для уменьшения длины кода.
Одним из таких методов является кодирование Хафмена. Он основан на использовании кодов различной длины для различных символов. Для максимально повторяющихся символов используют коды минимальной длины.
Построение кодовой таблицы происходит с использованием бинарного дерева. В корне дерева помещаются все символы и их суммарная частота повторения. Далее выбирается наиболее часто используемый символ и помещается со своей частотой повторения в левое поддерево. В правое поддерево помещаются оставшиеся символы с их суммарной частотой. Затем описанная операция проводится для всех вершин дерева, которые содержат более одного символа.
Само дерево может быть использовано в качестве кодовой таблицы для кодирования и декодирования текста. Кодирование осуществляется следующим образом. Для очередного символа в качестве кода используется путь от листа соответствующего символа к корню дерева. Причем каждому левому поддереву приписывается ноль, а каждому правому – единица.
Символ частота код

 D 5 0
D 5 0
C 3 10
A 1 110
B 1 111

ABCD, 10


C,3 AB,2