Вставка
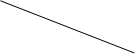
Рис.3.2. Разновидности методов разрешение коллизий
Методы открытой адресации метод цепочек
Методы разрешения коллизий
 |  | ||
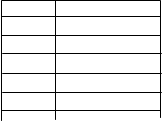
линейное квадратичное двойное
опробование опробование хеширование
 |  | ||
шаг = 1 шаг > 1
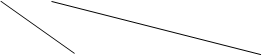
k1 k2 k3
k1 ¹ k2
h(k1)=h(k2)
k3 ¹ k1
h(k3)=h(k1)
Рис.3.3. Разрешение коллизий при добавлении элементов методом цепочек
Метод открытой адресации состоит в том, чтобы, пользуясь каким-либо алгоритмом, обеспечивающим перебор элементов таблицы, просматривать их в поисках свободного места для новой записи.
а) Линейное опробование
a à key1 a = h(key1)
адрес
key2 а = h(key2) + c*i
key1 ¹ key2
a=h(key1) = h(key2)
б) Квадратичное опробование
a à key1 a = h(key1)
адрес
key2 a = h(key2) + c*i + d*i 2
key1 ¹ key2
a=h(key1) = h(key2)
в) Двойное хеширование
a à key1 a = h1(key1)
адрес
a=h1(key2) + i*h2(key2)
key2
key1 ¹ key2
a=h1(key1) = h1(key2)
Рис.3.4. Разрешение коллизий при добавлении элементов методами открытой адресации.
Линейное опробование сводится к последовательному перебору элементов таблицы с некоторым фиксированным шагом
a=h(key) + c*i ,
где i – номер попытки разрешить коллизию. При шаге равном единице происходит последовательный перебор всех элементов после текущего.
Квадратичное опробование отличается от линейного тем, что шаг перебора элементов не линейно зависит от номера попытки найти свободный элемент
a = h(key2) + c*i + d*i 2
Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов.
Однако даже относительно небольшое число проб может быстро привести к выходу за адресное пространство небольшой таблицы вследствие квадратичной зависимости адреса от номера попытки.
Еще одна разновидность метода открытой адресации, которая называется двойным хешированием, основана на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хеш-функций
a=h1(key) + i*h2(key).
Опишем алгоритмы вставки и поиска для метода линейное опробование.
1. i = 0
2. a = h(key) + i*c
3. Если t(a) = свободно, то t(a) = key, записать элемент, стоп элемент добавлен
4. i = i + 1, перейти к шагу 2