Теоретическая модель СВИС на основе четырехуровневой среды
Уравнения для накачки и мощности спонтанного (ASE) излучения суперлюминесцентных источников, использующих четырехуровневые среды, аналогичны приведенным выше. Они отличаются только выражениями для населенностей  и
и  ). Кроме того, отсутствует поглощение частицами, находящимися на основном уровне (GSA). Если малы потери сигнала на рассеяние в волокне, что обычно выполняется, то коэффициенты усиления спонтанного излучения (ASE) во встречных направлениях практически идентичны. Следовательно, равны их выходные мощности:
). Кроме того, отсутствует поглощение частицами, находящимися на основном уровне (GSA). Если малы потери сигнала на рассеяние в волокне, что обычно выполняется, то коэффициенты усиления спонтанного излучения (ASE) во встречных направлениях практически идентичны. Следовательно, равны их выходные мощности:  . Это условие может быть использовано в качестве критерия сходимости при решении 2n + 1 связанных дифференциальных уравнений, что резко ускоряет сходимость этих уравнений.
. Это условие может быть использовано в качестве критерия сходимости при решении 2n + 1 связанных дифференциальных уравнений, что резко ускоряет сходимость этих уравнений.
Удобные приближенные выражения для мощностей прямого и обратного излучений четырехуровневого суперлюминесцентного источника (SFS) могут быть выражены через величину коэффициента усиления при однократном прохождения через волокно (а не через мощность накачки). Следуя такому подходу, мощности прямого и обратного излучений (ASE) 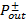 могут быть представлены в виде
могут быть представлены в виде
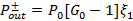 (8)
(8)
где  – усиление за один проход и
– усиление за один проход и  – безразмерный параметр, зависящий от спектральной формы линии усиления и
– безразмерный параметр, зависящий от спектральной формы линии усиления и  . При увеличении значения
. При увеличении значения  , параметр
, параметр  уменьшается от максимального значения, близкого к 1 (зависит от формы линии) до 0. Эта зависимость слаба по сравнения с
уменьшается от максимального значения, близкого к 1 (зависит от формы линии) до 0. Эта зависимость слаба по сравнения с  : для лоренцевской формы линии,
: для лоренцевской формы линии, 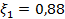 для
для  и
и 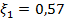 для
для  . Коэффициент
. Коэффициент  в ур.8 есть мощность спонтанного излучения, соответствующая одному фотону на моду
в ур.8 есть мощность спонтанного излучения, соответствующая одному фотону на моду
 (9)
(9)
где  - полная ширина на полувысоте (FWHM) спектра усиления слабого сигнала.
- полная ширина на полувысоте (FWHM) спектра усиления слабого сигнала.
Полученное выражение (8) может быть использовано для оценки эффективности источника излучения. Как следует из формулы (8) выходная мощность четырехуровневого суперлюминесцентного источника (SFS) растет с увеличением  немного медленнее, чем по линейному закону.
немного медленнее, чем по линейному закону.
Поскольку значения  порядка микроватт, то для получения выходной мощности на уровне милливатт требуется обеспечить большое усиление. Например, для перехода
порядка микроватт, то для получения выходной мощности на уровне милливатт требуется обеспечить большое усиление. Например, для перехода 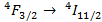 ионов
ионов  в кварцевом волокне,
в кварцевом волокне, 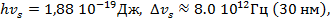 и
и 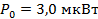 . При усилении в 30 дБ и в предположении гауссовской формы линии,
. При усилении в 30 дБ и в предположении гауссовской формы линии,  и выражение (8) дает выходную мощность
и выражение (8) дает выходную мощность  = 0,96 мВт в каждом из направлений.
= 0,96 мВт в каждом из направлений.
Если увеличивать мощность накачки, то  и мощность спонтанного излучения (ASE) будут увеличиваться экспоненциально. Однако, увеличение мощности спонтанного излучения приведет к насыщению усиления. Эффект насыщения приводит к тому, что при больших мощностях накачки выходная мощность растет линейно, как и в волоконном лазере-генераторе. Однако переход к насыщенному режиму в суперлюминесцентном источнике происходит более плавно, чем в лазере-генераторе.
и мощность спонтанного излучения (ASE) будут увеличиваться экспоненциально. Однако, увеличение мощности спонтанного излучения приведет к насыщению усиления. Эффект насыщения приводит к тому, что при больших мощностях накачки выходная мощность растет линейно, как и в волоконном лазере-генераторе. Однако переход к насыщенному режиму в суперлюминесцентном источнике происходит более плавно, чем в лазере-генераторе.
Можно получить выражения для зависимости выходной мощности от мощности накачки и для эффективности накачки, из которых следует, эффективность растет с увеличением мощности накачки. Максимальное значение эффективности (к.п.д.) накачки при величине квантовой эффективности равной 1 достигает следующего значения:
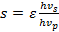 (10)
(10)
Где  для однопроходной схемы суперлюминесцентного источника и
для однопроходной схемы суперлюминесцентного источника и  для двухпроходной схемы.
для двухпроходной схемы.
В двухпроходном источнике максимальная эффективность преобразования накачки приближается к отношению энергий квантов излучения и накачки  . По существу, каждый поглощенный фотон накачки переходит в выходной фотон. Причина этого в том, что усиление и интенсивность сигнала настолько велики, что все возбужденные накачкой частицы в заимодействуют с сигнальным излучением и совершают вынужденные переходы, отдавая свою энергию световому полю. Как известно, эффективность накачки качественно спроектированного волоконного лазера также равна единице (
. По существу, каждый поглощенный фотон накачки переходит в выходной фотон. Причина этого в том, что усиление и интенсивность сигнала настолько велики, что все возбужденные накачкой частицы в заимодействуют с сигнальным излучением и совершают вынужденные переходы, отдавая свою энергию световому полю. Как известно, эффективность накачки качественно спроектированного волоконного лазера также равна единице ( ). Основное отличие состоит в том, что в волоконном лазере сигнальное излучение многократно проходит по резонатору, так что высокий к.п.д. достигается при меньших значениях мощности накачки, чем в двухпроходовых суперлюминесцентных источниках.
). Основное отличие состоит в том, что в волоконном лазере сигнальное излучение многократно проходит по резонатору, так что высокий к.п.д. достигается при меньших значениях мощности накачки, чем в двухпроходовых суперлюминесцентных источниках.
В однопроходном источнике  и эффективность преобразования составляет половину от эффективности двухпроходного источника. Результат ожидаем, поскольку практически одинаковые сигналы распространяются в двух противоположных направлениях. Таким образом, эффективность преобразования в однопроходном источнике, работающем по четырехуровневой схеме накачки, не может превышать 50%.
и эффективность преобразования составляет половину от эффективности двухпроходного источника. Результат ожидаем, поскольку практически одинаковые сигналы распространяются в двух противоположных направлениях. Таким образом, эффективность преобразования в однопроходном источнике, работающем по четырехуровневой схеме накачки, не может превышать 50%.
Шумы в источниках УСИ (ASE)
Отношение мощности сигнала к мощности шума (SNR) электрического сигнала, формирующегося фотодетектором при приеме неполяризованного излучения от теплового источника, в частности источником УСИ, определяется следующим выражением:
 ,
,
где  – среднее значение тока,
– среднее значение тока,  – ширина полосы фотоприемника,
– ширина полосы фотоприемника,  – ширина полосы излучения источника света. Первый член в знаменателе олпределяется вкладом шума Шоттки (мощность шума Шоттки
– ширина полосы излучения источника света. Первый член в знаменателе олпределяется вкладом шума Шоттки (мощность шума Шоттки  ). Второй член пропорционален избыточному шуму теплового источника (характерен для всех источников спонтанного излучения). Природа избыточных шумов – биения между Фурье-компонентами широкого оптического спектра сигнала. Если спектр источника достаточно широк (
). Второй член пропорционален избыточному шуму теплового источника (характерен для всех источников спонтанного излучения). Природа избыточных шумов – биения между Фурье-компонентами широкого оптического спектра сигнала. Если спектр источника достаточно широк ( >>
>> ), то SNR определяется шумом Шоттки, в противоположном случае – шумами биений. Во втором случае
), то SNR определяется шумом Шоттки, в противоположном случае – шумами биений. Во втором случае  . Таким образом, отношение сигнал-шум пропорционально ширине полосы источника и не зависит от тока фотоприемника. Иными словами, при использовании узкополосного теплового источника увеличить отношение сигнал-шум увеличением мощности сигнала невозможно. Приведенные формулы справедливы для всех видов источников излучения на основе спонтанного излучения.
. Таким образом, отношение сигнал-шум пропорционально ширине полосы источника и не зависит от тока фотоприемника. Иными словами, при использовании узкополосного теплового источника увеличить отношение сигнал-шум увеличением мощности сигнала невозможно. Приведенные формулы справедливы для всех видов источников излучения на основе спонтанного излучения.
Проиллюстрируем приведенные формулы зависимостями SNR от мощности сигнала для четырех типов источников: источника белого света (шума), двух суперлюминесцентных диодов (SLD) с длинами волн 0,82 мкм и 1,28 мкм и волоконного суперлюминесцентного источника излучения на основе волокна, легированного неодимом (длина волны 1,06 мкм). Как видно из рис. Спектр источника белого света широк настолько, что для всех значений мощности сигнала SNR определяется шумом Шоттки. В результате SNR пропорционален мощности сигнала. Зависимости SNR от мощности оказываются существенно иными для трех остальных источников излучения. При малом токе фотоприемника их SNR тоже ограничен шумом Шоттки и растет пропорционально мощности сигнала, но по мере увеличения тока (мощности) вклад шума биений возрастает. В пределе больших мощностей сигнала (тока фотоприемника) SNR становится не зависящим от мощности сигнала и достигает максимального значения в диапазоне 128-131 дБ. Экспериментальные точки находятся в хорошем соответствии с теоретическими кривыми [Langford 2001; Burns 1990].

Рис.12.2. Теоретические и экспериментальные зависимости отношения Сигнал-шум для различных широкополосных источников излучения.)
Стабильность среднего значения длины волны СВИС
По определению среднее значение длины волны источника света равно:

где  – плотность мощности на длине волны
– плотность мощности на длине волны  . Изменение среднего значения в первую очередь определяется вариациями пяти параметров: температуры
. Изменение среднего значения в первую очередь определяется вариациями пяти параметров: температуры  волокна, мощности накачки
волокна, мощности накачки  , длины волны накачки
, длины волны накачки  , состояния поляризации накачки
, состояния поляризации накачки  , мощности рассеянного назад излучения
, мощности рассеянного назад излучения  . Зависимость средней длины волны от этих параметров можно представить в следующем виде:
. Зависимость средней длины волны от этих параметров можно представить в следующем виде:

Первый член выражения ( ) – собственный температурный коэффициент активного волокна. Его происхождение – температурная зависимость спектра сечений излучения и поглощения. При изменение температуры изменяется спектр излучения и его средняя длина волны. Температурные зависимости спектра сечений излучения и поглощения могут существенно изменяться от образца к образцу. Величина этого коэффициента зависит также от длины волны и мощности накачки а также от длины волокна. Экспериментально измеренные значения составляют от -10 ппм/град до -15 ппм/град для неодимовых источников и от -3 ппм/град до +10 ппм/град для эрбиевых источников.
) – собственный температурный коэффициент активного волокна. Его происхождение – температурная зависимость спектра сечений излучения и поглощения. При изменение температуры изменяется спектр излучения и его средняя длина волны. Температурные зависимости спектра сечений излучения и поглощения могут существенно изменяться от образца к образцу. Величина этого коэффициента зависит также от длины волны и мощности накачки а также от длины волокна. Экспериментально измеренные значения составляют от -10 ппм/град до -15 ппм/град для неодимовых источников и от -3 ппм/град до +10 ппм/град для эрбиевых источников.
Происхождение второго члена ( ) – зависимость спектра усиленного спонтанного излучения от мощности накачки, связанная с насыщением усиления. Главный фактор, влияющий собственно на мощность накачки, - температура диода накачки и вариации тока накачки. Вклад этого фактора может быть сделан очень малым (менее 0,5 ппм) при использовании стандартных методов стабилизации тока накачки диодов (0,1 мА) и температуры (0,1 град С).
) – зависимость спектра усиленного спонтанного излучения от мощности накачки, связанная с насыщением усиления. Главный фактор, влияющий собственно на мощность накачки, - температура диода накачки и вариации тока накачки. Вклад этого фактора может быть сделан очень малым (менее 0,5 ппм) при использовании стандартных методов стабилизации тока накачки диодов (0,1 мА) и температуры (0,1 град С).
Третий член ( ) отражает зависимость спектра УСИ от длины волны накачки. Для уменьшения влияния этого члена следует выбирать длину волны накачки равной максиму поглощения, что устраняет линейную зависимость коэффициента поглощения от изменения
) отражает зависимость спектра УСИ от длины волны накачки. Для уменьшения влияния этого члена следует выбирать длину волны накачки равной максиму поглощения, что устраняет линейную зависимость коэффициента поглощения от изменения  .
.
Четвертый член определяет зависимость средней длины волны широкополосного источника излучения от поляризации накачки. Из-за поляризации накачки коэффициент усиления также оказывается зависящим от поляризации и, как следствие, спектр и средняя длина волны излучения также зависят от поляризации. Эффект зависимости средней длины волны от поляризации накачки может быть заметным. Так в широкополосном источнике на основе эрбиевого волокна при вариации поляризации по всем возможным состояниям средняя длина волны изменялась на 110 ппм [62].
Последний член выражения (…) связан с вариацией мощности обратного рассеяния от внешних устройств. Численное моделирование показало, что вклад этого члена может быть весьма значительным, например до 20 ппм/дБ для backward SFS с коэффициентом обратного рассеяния -40 дБ. Это означает необходимость использования изоляторов для ослабления влияния обратного рассеяния на среднюю длину волны.
Наиболее стабильным и эффективным широкополосным источником является суперлюминесцентный источник на основе эрбиевого волокна. Мощность таких источников излучения с центральной длиной волны 1,55 мкм и шириной полосы 10-30 нм может достигать сотен мВт. Типичная эффективность таких источников превышает 50%, для накачки их используются относительно маломощные полупроводниковые лазеры (менее 40 мВт) и они очень компактны. Они могут выпускаться в виде источников излучения с высокой степенью поляризации и очень высокой стабильностью центральной длины волны порядка 1 ппм.
Литература.
1. Оптическая связь…
2. Langford N. «Narrow-Linewidth Fiber Lasers» in Rare-Earth-Doped Fiber Lasers and Amplifiers, edityd by M. J. F. Digonnet (2001)
3. W. K. Burns, R. P. Moeller, A. Dandridge. Excess noise in fiber gyroscope sources. IEEE Photon. Technol. Lett. 2:606–608 (1990).
52. D. W. Hall, R. A. Haas, W. F. Krupke, M. J. Weber. Spectral and polarization hole burning
in neodymium glass lasers. IEEE J. Quant. Electron. 19:1704–1717 (1983).
53. V. J. Mazurczyk, J. L. Zyskind. Polarization dependent gain in erbium doped-fiber amplifiers.
IEEE Photon. Technol. Lett. 6:616–618 (1994).
54. J. L. Wagener, D. G. Falquier, M. J. F. Digonnet, H. J. Shaw. A Mueller Matrix Formalism
for Modeling Polarization Effects in Erbium-Doped Fiber, J. Lightwave Technol. 16, No. 2,
200–206 (Feb. 1998).
55. D. G. Falquier, J. L. Wagener, M. J. F. Digonnet, H. J. Shaw. Polarized Superfluorescent Fiber
Source. Opt. Lett. 22, No. 3, 160–162 (Feb. 1997).