Диагностическая матрица в методе Байеса
Таблица 1
Диагностическая матрица.
Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу (табл. 1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков при различных диагнозах. Если признаки двухразрядные (простые признаки «да—нет»), то в таблице достаточно указать вероятность появления признака P(kj,/Di).
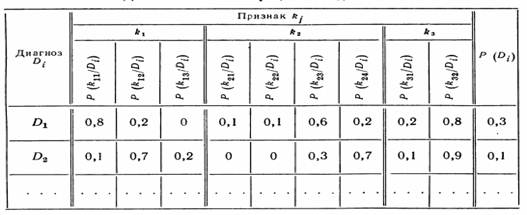
В диагностическую матрицу включены априорные вероятности диагнозов. Процесс обучения в методе. Байеса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти ЭВМ следует хранить не только значения вероятности, но и следующие величины: N — общее число объектов, использованных для составления диагностической матрицы; Nt — число объектов с диагнозом D; Nij — число объектов с диагнозом D, обследованных по признаку Kj.
Решающее правило — правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса объект с комплексом признаков К* относится к диагнозу с наибольшей (апостериорной) вероятностью (Апостерио́рная вероя́тность - условная вероятность случайного события при условии того, что известны данные, полученные после опыта)
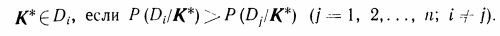 (3.19)
(3.19)
Символ Є, применяемый в функциональном анализе, означает принадлежность множеству. Условие (3.19) указывает, что объект, обладающий данной реализацией комплекса признаков К* или, реализация K* принадлежит диагнозу (состоянию) D. Правило (3.19) обычно уточняется введением порогового значения для вероятности диагноза:
P(Di/K*)>Pi, (3.20)
где Pi — заранее выбранный уровень распознавания для диагноза D. При этом вероятность ближайшего конкурирующего диагноза не выше 1 — Pi . Обычно принимается Pi > 0,9. При условии
P(Di/K*)≤Pi, (3.21)
решение о диагнозе не принимается(отказ от распознавания) и требуется поступление дополнительной информации.
Процесс принятия решения в методе Байеса при расчете на ЭВМ происходит достаточно быстро.
Как указывалось, методу Байеса присущи некоторые недостатки, например погрешности при распознавании редких диагнозов. При практических расчетах целесообразно провести диагностику и для случая равновероятностных диагнозов, положив
P(D)i=1/n. (3.22)
Тогда наибольшим значением апостериорной вероятности будет обладать диагноз D, для которого P(D)i максимальна:
Иными словами, устанавливается диагноз D, если данная совокупность признаков чаще встречается при диагнозе D, чем при других диагнозах. Такое решающее правило соответствует методу максимального правдоподобия. Из предыдущего вытекает, что этот метод является частным случаем метода Байеса при одинаковых априорных вероятностях диагнозов. В методе максимального правдоподобия «частые» и «редкие» диагнозы равноправны.