Статистические показатели
Лекция 5
Статистический показатель (СП) – это обобщающая количественная характеристика изучаемого объекта или его свойства.
В зависимости от методов расчета обобщающие показатели могут быть абсолютными, относительными или средними величинами.
Абсолютные величины
СП, выражающие размеры (объемы, уровни) социально-экономических явлений в единицах меры, веса, объема, протяженности, площади, стоимости и т.д., называются абсолютными статистическими величинами. Они всегда имеют определенные единицы измерения.В самой общей классификации их можно свести к трем типам:
- натуральные;могут быть простые,выражаются в мерах веса, объема, длины, площади и т.д., и сложные – киловатт-час, тонно-километр и т.д. В ряде случаев применяются условно натуральные единицы измерения.
- денежные (стоимостные);
- трудовые.
Относительные величины
Относительными показателями называются СП, определяемые как отношение сравниваемой АВ к базе сравнения.
ОВ = Числитель – сравниваемая величина, текущая или отчетная величина/ Знаменатель – основание, база сравнения или базисная величина.
Сопоставляемые величины могут быть одноименными и разноименными.
Если сравниваются одноименные величины, то ОП выражаются:
ü основание 1 – коэффициенты;
ü база сравнения 100 – проценты;
ü база сравнения 1000 – промилле;
ü база сравнения 10000 – продецимилле.
При сопоставлении разноименных величин наименования ОВ образуются от наименований сравниваемых величии.
В зависимости от задач, содержания и значения выражаемых количественных соотношений различают:
ОППЗ – относительный показатель планового задания показывает, во сколько раз или на сколько процентов должна возрасти (снизиться) величина показателя по плану в сравнении с его уровнем в предыдущем периоде.
ОПВП – относительный показатель выполнения плана – отношение фактического уровня показателя в отчетном (текущем) периоде к плановому заданию того же периода.
ОПД – относительный показатель динамики характеризует изменения показателя во времени.
ОПД=ОППЗ∙ОПВП
ОПС– относительные показатели структуры – это отношение части к целому.
ОПК– относительные показатели координации – это соотношение между частями одного целого.
ОПИ – относительные показатели интенсивности показывают степень распространения явления в определенной среде, уровень его развития., разновидность – ОПУЭР;
ОПСр– относительные показатели сравнения – это отношение одного и того же показателя за один и тот же период (момент) времени, но по различным объектам или разным территориям.
Средние величины
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления в конкретных условиях места и времени.
Все средние делятся на два класса:
1. степенные средние – средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая; Степенные средние исчисляются в двух формах – простой и взвешенной. Правило мажорантности.
На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
ИСС= отношение суммарного значения или объема осредняемого признака к числу единиц или объему совокупности.
2. структурные средние величины – мода и медиана.
Показатели вариации и способы их расчета
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией (изменчивостью) признаков, характеризующих отдельные единицы совокупности. При характеристике вариации признаков используют ряд показателей.
Абсолютные показатели вариации:
· Размах вариации;
· Среднее линейное отклонение;
· Дисперсия;
· Среднеквадратическое отклонение.
Абсолютные показатели, кроме дисперсии, измеряются в тех же единицах, что и сам признак.
Относительные показатели вариации:
· Коэффициент осцилляции;
· Относительное линейное отклонение;
· Коэффициент вариации.
Относительные показатели чаще всего выражаются в процентах
Размах вариации характеризует границы вариации изучаемого признака и определяется по формуле
R = xmax - xmin,
где xmax – максимальное значение варьирующего признака;
xmin – минимальное значение варьирующего признака.
Среднее линейное отклонение 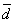 вычисляется по следующим формулам:
вычисляется по следующим формулам:
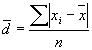 или
или 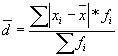 .
.
Дисперсия  - средняя из квадратов отклонений вариантов значений признака от их средней величины.
- средняя из квадратов отклонений вариантов значений признака от их средней величины.
Дисперсия рассчитывается по следующим формулам:
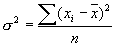 или
или  .
.
Среднее квадратическое отклонение  представляет собой корень квадратный из дисперсии.
представляет собой корень квадратный из дисперсии.
Коэффициент вариации рассчитывается по формуле:
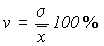
Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической. По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Коэффициент вариации важен в тех случаях, когда нужно сравнивать средние квадратические отклонения, выраженные в разных единицах измерения.