Влияние перемещения грузов на посадку и остойчивость судна

Для определения посадки и остойчивости судна при произвольном перемещении грузов необходимо рассмотреть раздельно вертикальное, поперечное горизонтальное и продольное горизонтальное перемещение.

Необходимо помнить, что в начале следует выполнить расчеты, связанные с изменением остойчивости (вертикальное перемещение, подъем груза)

3.6.1 Вертикальное перемещение груза (рис.3.9) из точки 1 в точку 2 не создает момента, способного наклонить судно, и следовательно, его посадка не меняется (если только остойчивость судна при этом остается положительной). Такое перемещение приводит только к изменению по высоте положения центра тяжести судна. Можно сделать вывод, что данное перемещение приводит к изменению остойчивости нагрузки при неизменной остойчивости формы. Перемещение центра тяжести определяется по известной теореме теоретической механики:

δz_g = 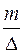(z₂ – z₁),

 

где m – масса перемещаемого груза,

Δ – масса судна,

z₁ и z₂ – аппликаты ЦТ груза до и после перемещения.

Приращение метацентрических высот составит:

δh = δН = – δz_g= – 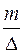(z₂ – z₁).

Судно после перемещения груза будет иметь поперечную метацентрическую высоту:

h₁ = h + δh.

Вертикальное перемещение груза не приводит к значительному изменению продольной метацентрической высоты, ввиду малости δН по сравнению с величиной Н.

 

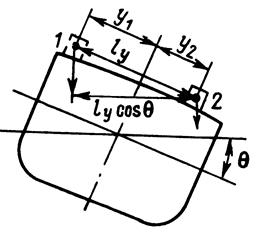
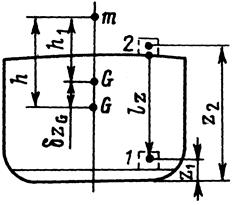
Рисунок 3.9 – Вертикальное Рисунок 3.10 – Поперечное горизонтальное

перемещение груза перемещение груза

 

3.6.2 Подвешенные грузыпоявляются на судне в результате подъема груза из трюма на палубу, приемом улова, выборкой сетей с помощью грузовых стрел и т.п. Влияние на остойчивость судна подвешенный груз (рис.3.9) оказывает аналогично вертикально перемещенному, только изменение остойчивости происходит мгновенно в момент отрыва его от опоры. При подъеме груза, когда натяжение в шкентеле станет равным весу груза, происходит мгновенное перемещение центра тяжести груза из точки 1 в точку подвеса (точку 2) и дальнейший подъем не будет оказывать влияние на остойчивость судна. Оценить изменение метацентрической высоты можно по формуле

δh = – 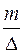l,

где l = (z₂ – z₁) – первоначальная длина подвеса груза.

На небольших судах, в условиях пониженной остойчивости, подъем груза судовыми стрелами может представлять значительную опасность.

3.6.3 Поперечное горизонтальное перемещение грузамассой m (рис.3.10) приводит к изменению крена судна в результате возникающего момента m _кр с плечом (y₂ – y₁)cosΘ.

m _кр = m (y₂ – y₁) cosΘ = m l_y cosΘ,

где y₁ и y₂ – ординаты положения ЦТ груза до и после перемещения.

Учитывая равенство кренящего m_кр и восстанавливающего моментов m_Θ, используя метацентрическую формулу остойчивости, получим: Δh sinΘ = m l_y cosΘ, откуда

tgΘ = m l_y /Δh.

Учитывая, что углы крена небольшие, можно считать, что

tgΘ = Θ = Θ⁰/57,3⁰,

и формула примет вид:

Θ⁰ = 57,3⁰ m l_y /Δh.

Если до перемещения груза судно имело крен, то в данной формуле угол следует рассматривать как приращение δΘ⁰

3.6.4 Продольное горизонтальное перемещение груза(рис.3.11) приводит к изменению дифферента судна и поперечной метацентрической высоты. По аналогии с предыдущим случаем при М_Ψ = М_диф, получим:

tg Ψ = m l_х /ΔН, или

Ψ⁰ = 57,3⁰ m l_х /ΔН.

На практике продольные наклонения чаще оценивают величиной дифферента D_f = Ψ⁰ L /57,3⁰, тогда

D_f = m l_х L /ΔН,

где L – длина судна.

Используя момент, дифференующий судно на 1 см (входящий в состав грузовой шкалы и КЭТЧ),

m_Д = 0,01 γV Н/ L (кН м/см) ;

m_Д = 0,01 ΔН/ L = 0,01 ΔR / L (т м/см),

так как Н » R, получим

D_f = m l_х / m_Д (см).

 

 

Рисунок 3.11 –Продольное горизонтальное перемещение груза

 

Изменение осадок при продольном перемещении груза:

δd_н = (0,5L – x_f ) Df/ L,

δd_к = – (0,5L + x_f ) Df/ L.

Тогда новые осадки судна будут:

d_н1 = d_н + δd_н = d_н + (0,5L – x_f ) Df/ L,

d_к1 = d_к + δd_к = d_к – (0,5L + x_f ) Df/ L;

где x_f – абсцисса оси продольных наклонений.