Построение множественного уравнения регрессии

Теперь построим уравнение множественной регрессии. В нем результативный признак (у) будет зависеть не от одного факторного признака, а от двух (х₁, х₂).

Пример 8.4 – В таблице 8.6 представлены данные о душевом доходе и потреблении мяса семей различного состава.

 

Таблица 8.6 - Расчет параметров уравнения множественной регрессии

Номер домохозяйства	Средний доход на члена семьи за месяц, усл. ден. ед. ()	Число ленов семьи ()	Душевое потребление мяса за месяц, кг ()
			3,0	210,0	12,0				3,0
			3,3	280,5	13,2				3,5
			4,2	378,0	12,6				4,0
			5,0	500,0	15,0				4,6
			4,5	562,5	9,0				5,5
			6,8	1020,0	13,6				6,4
			6,2	806,0	6,2				5,9
			7,0	1120,0	7,0				7,0
итого			40,0	4877,0	88,6				40,0
в среднем	113,75	2,5	5,0	609,6	11,1	253,75		7,5	5,0

 

Предполагая, что связь между у, х₁и х₂прямолинейная, воспользуемся методом наименьших квадратов и подставим данные таблицы в систему нормальных уравнений:

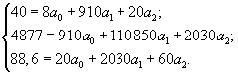
Решим ее.

Для решения системы нормальных уравнений разделим все члены уравнений на коэффициент при а₀

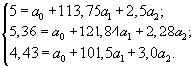
Вычтем теперь из первого уравнения второе и третье и получим

-0,36 = -8,06а₁ + 0,27а₂;

0,57 = 12,25а₁ - 0,5а₂.

Разделим все члены уравнений на коэффициенты при а₂ и вычтем из первого уравнения второе

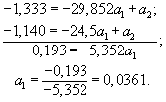
Подставив значение параметра а₁ в уравнение, получим

-1,140 = -24,5 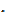0,0361 + а₂,

откуда

а₂ = -1,140 + 0,8844 = 0,2556.

Аналогично определяем значение параметра а₀, которое будет равно 1,5327.

Получим:

а₀ = 1,5327; а₁ = 0,0361; а₂ = 0,2556.

Уравнение множественной регрессии, характеризующее зависимость потребления мяса от душевого дохода и числа членов семьи, будет иметь вид

Параметр а₁ показывает, что с ростом дохода на одного члена семьи на 1 усл. ден. ед. расходы на потребление мяса увеличиваются в среднем на 0,0361 усл. ден. ед., а параметр а₂ показывает, что с увеличением размера семьи на 1 человека потребление мяса уменьшается в среднем на 0,2556 кг в расчете на одного человека.

Подставим в уравнение множественной регрессии эмпирические значения х₁и х₂, получим теоретические значения(см. последнюю графу таблицы).

При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Для нашего примера коэффициент множественной корреляции имеет вид

 

где- парные коэффициенты корреляции.

 

Коэффициент множественной корреляции может принимать значения в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.

Рассчитаем коэффициент множественной корреляции (таблица 8.7).

 

Таблица 8.7 - Расчет коэффициента множественной корреляции

Для определения парных коэффициентов корреляции вычислим:

Парные коэффициенты корреляции определяются по следующим формулам:

Подставим найденные значения в формулу коэффициента множественной корреляции

Сравнивая парные коэффициенты корреляции с коэффициентом множественной корреляции, мы видим, что связь между результативным признаком (у) и двумя факторами (х₁ и х₂) является более полной, чем с каждым фактором в отдельности.

Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х₁ и у при постоянном х₂ исчисляется по следующей формуле:

 

 

Частный коэффициент корреляции при изучении зависимости у от х₂ при постоянном х₁ определяется по формуле

 

 

В нашем примере частный коэффициент корреляции между у и х₁ при неизменном значении х₂ равен

 

 

Частный коэффициент корреляции между у и х₂ при неизменном значении фактора х₁ равен

 

Если сравнить исчисленные коэффициенты частной корреляции с соответствующими коэффициентами парной корреляции, то окажется, что последние значительно больше первых, т. е. они преувеличивают меру связи между результативным и факторным признаком. Это объясняется тем, что факторы взаимно коррелируют между собой.

Коэффициенты же частной корреляции определяют действие каждого фактора при неизмененном значении остальных факторов. Поэтому они более точно определяют тесноту связи.