III. Переход к следующему опорному решению

 

При переходе от одного опорного решения к другому между множествами базисных и свободных переменных происходит взаимообмен переменными: одна из базисных переменных переходит в разряд свободных, а одна из свободных переменных переходит в разряд базисных.

Точка	Свободные переменные (нулевые)	Базисные переменные (ненулевые)
A	x1 x2	x3 x4 x5
B	x1 x5	x3 x4 x2
C	x4 x5	x3 x1 x2

 

Например, для рассматриваемой задачи:

 

 

Для перехода к лучшему опорному решению следует увеличивать от исходного нулевого значения ту свободную переменную, которая в целевой функции имеет положительный коэффициент.

 

Однако увеличивать эту переменную следует так, чтобы значения базисных переменных оставались неотрицательными (так, чтобы не выйти за пределы допустимых решений).

Если в целевой функции несколько переменных имеют положительный коэффициент, то для обмена следует выбирать ту свободную переменную, которой соответствует . Это в большинстве случаев позволяет быстрее получить оптимальное решение.

 

Пример (продолжение).

 

6) Переходим к другому опорному решению.

 

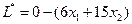
Имеющееся решение можно улучшить, если увеличить переменную 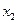, но только до 4, иначе 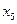станет меньше 0.

Выбранную свободную переменную обменивают с такой базисной, которая при увеличении этой свободной переменной первой обращается в ноль.

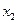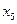То есть меняем местами переменные и (переменную 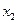введём в базис, а 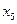сделаем свободной).

, .

 

,

.

 

,

.

 

,

.

 

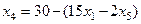Получим следующую систему уравнений:

 

.

 

Полагаем , тогда , , , (на графике - точка ).

 

7) Проверяем опорное решение на оптимальность.

Т.к. в целевой функции имеется положительный коэффициент при свободной переменной 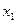, то решение не является оптимальным.

 

8) Переходим к следующему опорному решению.

Переменную 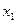переведём в разряд базисных, а переменную - в разряд свободных.

,

.

 

,

 

.

 

,

 

.

 

,

 

.

 

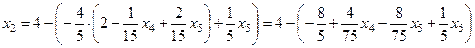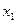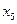Базисные переменные , , выражаются через , следующим образом:

.

Полагаем , тогда , , , (на графике – точка ).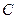

Это решение является оптимальным, т.к. увеличение свободных переменных не приведёт к уменьшению (коэффициенты при свободных переменных в целевой функции отрицательны).

Максимум исходной целевой функции равен: .

 

Ответ: при , .

 

 

Симплексные таблицы

Процедура пересчёта коэффициентов в системе ограничений и в целевой функции при замене свободной переменной на базисную может осуществляться с помощью симплексной таблицы.

Пусть решается задача на отыскание минимума функции

при ограничениях

,

где - дополнительные переменные, которые выбираются в качестве базисных.

, или

Исходные данные заносим в первую симплексную таблицу.

			С в о б о д н ы е п е р е м е н н ы е
		Bi	x1	x2		xk		xn
Б а з и с н ы е п е р е м е н н ы е	xn+1	b1
xn+2	b2
	. .	. .	. .	. .	. .	. .	. .
xr	br
	. .	. .	. .	. .	. .	. .	. .
xn+m	bm
	L		s1	s2		sk		sn

 

В левом столбце таблицы () записываются свободные члены . В основную часть таблицы (начиная со второго столбца и первой строки) заносятся коэффициенты при свободных переменных.

В последней строке таблицы указываются коэффициенты целевой функции, взятые из выражения в скобках.

 

 

Далее таблица преобразуется по определённым правилам.

I. Выбирается максимальное (любое) положительное число в нижней строке симплексной таблицы (кроме столбца ’’).

Если положительного числа нет, то опорное решение является оптимальным, минимум целевой функции достигнут (в левом нижнем углу таблицы), свободные переменные равны 0, базисные переменные принимают значения (первый столбец).

II. Допустим, что правило I даёт нижний элемент -го столбца (столбец с номером называется ключевым).

Составляются все неотрицательные отношения элементов первого столбца (столбца свободных членов) к элементам ключевого столбца, другими словами, все отношения, для которых .

Элемент, скажем , который даёт наименьшее отношение , называется разрешающим, а строка с номером называется ключевой.

Если все элементы -го столбца отрицательны или равны нулю, то задача не имеет оптимального решения (целевая функция не ограничена снизу).

III. Новая таблица строится следующим образом:

1) меняются местами обозначения ключевой строки и ключевого столбца (и), при этом остальные обозначения остаются без изменений;

2) разрешающий элемент заменяется обратной величиной

, где - элементы новой таблицы;

3) каждый элемент ключевой строки заменяется его отношением к разрешающему элементу , , , ;

(новая строка получается из старой делением на разрешающий элемент )

4) каждый элемент ключевого столбца заменяется его отношением к разрешающему элементу, взятому с противоположным знаком

, , , ;

 

5) все остальные элементы таблицы заменяются элементами вида

.

Последнее правило можно записать более коротко:

.

 

Далее переходим к п.Iалгоритма.

 

 

Пример 1. ОЗЛП:

 

	Bi	x1	x2
x3				100:1=100
x4				1100:20=55
x5				160:4=40
L*

 

	Bi	x1	x5
x3				60:=80
x4			-5	300:5=60
x2				40:=160
L*	-4800		-30

 

	Bi	x4	x5
x3
x1			-1
x2
L*	-5400	-2	-20

 

 

 

Ответ: при