II. Проверка опорного решения на оптимальность

Теорема. Опорное решение является оптимальным, если коэффициенты 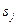при свободных переменных в целевой функции 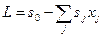отрицательны или равны нулю.

Если полученное опорное решение не оптимально, то нужно перейти к другому опорному решению.

 

Пример (продолжение).

 

5) Проверим, является ли полученное опорное решение оптимальным.

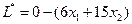
Т.к. коэффициенты при свободных переменных 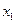и 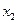положительны, то это решение не является оптимальным.