I. Нахождение первоначального опорного решения

Алгоритм симплекс-метода

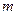Рассмотрим основную задачу линейного программирования (ОЗЛП): найти неотрицательные значения переменных , удовлетворяющие условиям-равенствам и обращающие в минимум линейную функцию этих переменных.

 

(1)

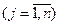(2) . (3)

Положим, что все уравнения системы (2) являются линейно независимыми.

Равенства называются линейно независимыми, если никакое из них нельзя получить из других путём умножения на какие-то коэффициенты и суммирования, т.е. никакое из них не является следствием остальных.

В линейной алгебре доказывается, что систему из 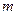независимых равенств с 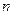переменными 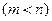всегда можно разрешить относительно каких-то 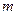переменных (называемых базисными) и выразить их через остальные 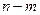переменных (называемых свободными).

Свободным переменным можно придавать какие угодно значения, не нарушая условий (2) и (3).

Если свободные переменные приравнять к нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (2) будет являться опорным решением ЗЛП.

 

Пример.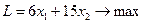

 

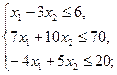
1) Приводим данную задачу к ОЗЛП.

.

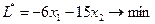
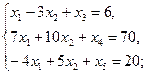
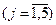2) Разделим переменные на базисные и свободные.

Количество базисных переменных равно числу уравнений в системе ограничений: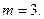

Количество свободных переменных:

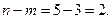
Выберем в качестве базисных переменных те дополнительные переменные, которые добавили к неравенствам, чтобы получить равенства:

.

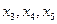Т.к. каждая из этих переменных входит в одно из уравнений системы ограничений с коэффициентом, равным 1, а во все остальные уравнения – с коэффициентом, равным 0, то они легко выражаются через переменные 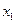и .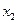

 

3) Выразим базисные переменные и целевую функцию через свободные переменные.

 

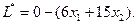
4) Полагаем свободные переменные, равными нулю.

тогда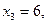

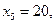
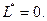
Так как 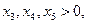то полученное решение является опорным (на графике – точка ).