Геометрическая интерпретация идеи симплекс-метода
Идея симплекс-метода
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗЛП
Использование графического метода (когда оптимальное решение находится с помощью геометрических построений) возможно только при решении ЗЛП с двумя переменными.
При бóльшем числе переменных необходимо применение алгебраического аппарата.
Общий метод решения ЗЛП называется симплексным (или симплекс-методом).
При решении ЗЛП графическим методом было отмечено, что оптимальному решению всегда соответствует одна из угловых точек многоугольника (многогранника) решений. Именно этот результат и положен в основу симплекс-метода.
Однако исследовать все вершины многогранника решений (опорные решения) очень сложно. Отсюда естественно стремление найти такой способ перехода от данной вершины к другой, при котором значение целевой функции будет меньше (задача на минимум) или больше (задача на максимум), чем в предыдущем случае.
Переходы от одной угловой точки к другой необходимо осуществлять до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Итак, симплексный метод предполагает:
1) умение находить начальное опорное решение;
2) наличие признака оптимальности опорного решения;
3) умение переходить к лучшему (или, по крайней мере, не худшему) опорному решению.
|
Пусть имеется задача на отыскание минимального значения целевой функции
.
На рисунке изображён многоугольник её решений.
Допустим, что найдено первоначальное опорное решение, соответствующее угловой точке 
. Тогда прямая 
проходит через точку , и 
имеет значение 
.
Следующий шаг симплекс-метода обеспечивает переход в точку 
, где целевая функция принимает значение 
.
|
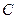, далее – к точке 
, в которой целевая функция достигает минимального значения.
Симплексный метод обеспечивает движение по соседним угловым точкам многоугольника решений, связанным с уменьшением (увеличением) значения целевой функции.
Две угловые точки называются соседними, если они расположены на одном ребре многоугольника решений.