Байесовской стратегии.
Геометрическая интерпретация выбора
Пусть имеется игра с двумя состояниями природы L(V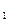 , a) и L(V
, a) и L(V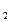 , a)
, a)
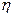 (a) — смешанная стратегия статистика.
(a) — смешанная стратегия статистика.
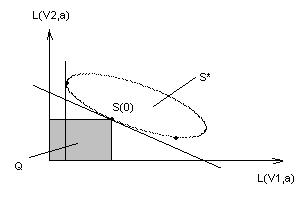
Построим вспомогательное множество, состоящее из всех точек, лежащих левее и ниже S .
.
Считают, что множества S* и Q выпуклые и не пересекаются. Следовательно, можно провести прямую, разделяющую два этих множества. Эта прямая должна проходить через точку S . Эта прямая является опорной.
. Эта прямая является опорной.
Эта прямая:
1. Вертикальная;
2. Горизонтальная;
3. Имеет отрицательный наклон
Уравнение y = -kx + c, k>0
ax + by = c’*k + 1>0
a = k/(k+1); b = 1/(k+1); c’ = c/(k+1); a, b, c >0; a + b = 1
Величины a и b можно толковать как вероятности состояний природы
a = 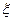 (V
(V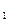 ) = W; b =
) = W; b = 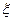 (V
(V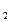 ) = 1-W; (1-W)*y = c’.
) = 1-W; (1-W)*y = c’.
Т. о. величина c’ определяет средние байесовские потери статистика L(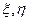 ) при априорных вероятностях W и (1-W) состояний природы. Нетрудно убедиться в том, что эти значения c’ являются минимальными для всех значений L(
) при априорных вероятностях W и (1-W) состояний природы. Нетрудно убедиться в том, что эти значения c’ являются минимальными для всех значений L(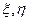 ), т. к. при c’’ > c’(справа от прямой) эта прямая не будет иметь общих точек с нижней левой границей и будет соответствовать недопустимым стратегиям статистика. Если c’’ < c’, то тоже не будет общих точек с S* (слева от прямой).
), т. к. при c’’ > c’(справа от прямой) эта прямая не будет иметь общих точек с нижней левой границей и будет соответствовать недопустимым стратегиям статистика. Если c’’ < c’, то тоже не будет общих точек с S* (слева от прямой).
Т. о. можно утверждать, что каждая допустимая стратегия статистика является байесовской при некоторых вероятностях состояния природы.
Можно показать обратную задачу: пусть известны W и (1-W) — вероятности состояния природы, V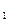 и V
и V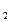 . Требуется определить точку S
. Требуется определить точку S
 S*, соответствующую этим значениям вероятности. Тогда априорные вероятности W и (1-W) определят некоторую прямую W*x + (1-W)*y = c/
S*, соответствующую этим значениям вероятности. Тогда априорные вероятности W и (1-W) определят некоторую прямую W*x + (1-W)*y = c/
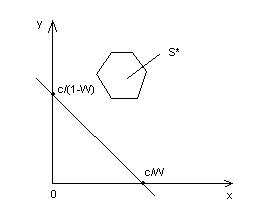 x/(1-W) + y/W = c’
x/(1-W) + y/W = c’
c’ = c/W(1-W), W (0,1)
(0,1)
Если менять C’, то прямая будет перемещаться параллельно самой себе.
Далее рассмотрим выпуклую линейную оболочку дискретного множества чистых стратегий статистика S*.
Нижняя левая граница определяется двумя линиями. Меняя C’ можно добиться того, чтобы эта прямая касалась множества S*.
S* — многоугольник с вершинами, соответствующими чистым стратегиям статистика. В этом случая прямая должна проходить хотя бы через одну из его вершин. Следовательно, для любых чисел W и (1-W), являющихся априорными вероятностями состояния природы, всегда существует хотя бы одна байесовская стратегия статистика, которая является чистой. Это обстоятельство при поиске байесовских решений позволяет ограничиться анализом допустимых чистых стратегий статистка, а не рассматривать бесконечное число его смешанных стратегий.