Земной эллипсоид

Геоид

Понятия о фигуре и размерах земли

Для определения положения точек и направлений на земной поверхности необходимо знать геометрическую форму и размеры Земли.

Земля имеет сложную фигуру. Сложность этой фигуры обусловлена наличием материков (29 % поверхности Земли) и Мирового океана с морями (71 %), а также неравномерным распределением масс в теле Земли.

За фигуру Земли принимается геоид. Геоидом называется фигура, ограниченная уровенной поверхностью, совпадающей в открытых морях и океанах с их спокойной поверхностью и мысленно продолженной под материками, (рисунок 1).

 

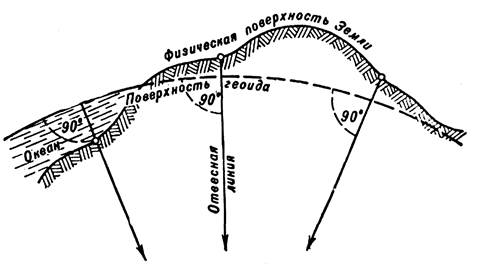
Рисунок 1 – Уровенная поверхность

 

Уровенная поверхность в каждой точке пересекает направление отвесной линии (направление силы тяжести) под прямым углом.

Направление отвесной линии в каждой точке зависит от распределения масс в теле Земли. Следовательно, геоид учитывает эту неравномерность распределения масс и тем самым наиболее правильно представляет фигуру Земли.

От поверхности геоида (от уровня моря) ведется отсчет высот точек. Использовать же геоид для обработки линейных и угловых геодезических измерений не представляется возможным, так как он не является правильным геометрическим телом, поверхность которого можно было бы выразить математической формулой. Поэтому поверхность геоида заменяется наиболее близкой к ней поверхностью земного эллипсоида (рисунок 2).

 

 

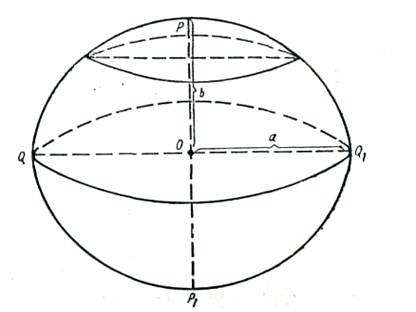
Рисунок 2 – Эллипсоид вращения

Размеры земного эллипсоида устанавливаются из определений размеров Земли.

Форма и размеры земного эллипсоида определяются его эле­ментами: большой а и малой b полуосями и полярным сжатием α, которые между собой связаны соотношением

.

Обычно для земного эллипсоида указываются величины большой полуоси и полярного сжатия. Значения этих величин вычисляются, как правило, на основе многочисленных геодезических измерений, выполненных на территории одной или нескольких стран. Учеными разных стран было проведено более 60 определений раз­меров земного эллипсоида. В Советском Союзе до 1946 г. использовался эллипсоид Бесселя. С 1946 г. принят эллипсоид Красовского, у которого большая (экваториальная) полуось а = 6378245 м, малая (полярная) полуось b = 6356863 м и полярное сжатие α = 1 : 298,3.

С развитием ракетного оружия и космических летательных аппаратов возникла необходимость в знании размера земного эллипсоида, наилучшим образом представляющего фигуру Земли в целом. Такой эллипсоид называется общим земным эллипсоидом.

Размеры общего земного эллипсоида и его положение в теле Земли определяют так, чтобы:

1) объем его был равен объему геоида;

2) плоскость экватора и малая ось его совпадали соответственно с плоскостью экватора и осью вращения Земли;

3) сумма квадратов уклонений по высоте поверхности геоида от поверхности общего земного эллипсоида была наименьшей.