Верхние и нижние цены в S-игре

S-игра

Основная теорема антагонистических игр.

 

Играм, в которых у первого игрока конечное число стратегий, можно дать полезную геометрическую интерпретацию. Пусть задана игра 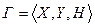с матрицей платежей .

Можно рассмотреть множество векторов:

….. .

Игра, заданная множеством точек , получила название S-игры.

Правила S-игры следующие: второй игрок выбирает одну из точек , а первый игрок выбирает i-ую координату этой точки . При этом выигрыш первого игрока, соответственно проигрыш второго, будет равен значению i-ой координаты точки , т.е. :

.

Нетрудно видеть, что S-игра эквивалентна обычной игре в нормальной форме 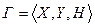, т.к. выбор точки из множества эквивалентен выбору стратегии 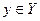, а выбор координаты этой точки эквивалентен выбору стратегии .

Если число стратегий первого игрока равно двум, то S-игра имеет наглядное геометрическое изображение, т.к. точки множества будут в этом случае точками плоскости (платежная матрица будет иметь вид:

, в которой столбцы заменяются на точки с координатами ).

 

Пример:

Рассмотрим игру . Эквивалентная S - игра содержит 5 точек: , , , , . Геометрическое изображение этой игры приведено на рисунке.

 

Обозначим через выпуклую оболочку конечного множества точек . S-игра эквивалентна обычной игре в чистых стратегиях. Доказывается, что эта эквивалентность сохраняется и для смешанных стратегий.

Теорема. Любая смешанная стратегия второго игрока может быть представлена точкой, принадлежащей выпуклой оболочке , и наоборот, любая точка может рассматриваться как некоторая смешанная стратегия второго игрока.

Доказательство. Рассмотрим смешанные стратеги игроков и . При использовании этих смешанных стратегий проигрыш второго игрока

, где .

Обозначим через S точку в m-мерном пространстве с координатами :

;

………………………….

.

Учитывая, что , это выражение можно записать в виде векторного соотношения

.

Видим, что S есть не что иное, как средневзвешенное точек с весами , а следовательно, S есть некоторая точка, принадлежащая выпуклой оболочке . Таким образом, каждой стратегии второго игрока будет соответствовать некоторая точка, принадлежащая выпуклой оболочке , и задание этой точки равносильно заданию смешанной стратегии второго игрока.

Справедливо и обратное. Так как любая точка S, принадлежащая выпуклой оболочке , может быть представлена как средневзвешенное точек

, определяющих выпуклую оболочку , то для каждой точки найдутся такие веса , задание которых определит смешанную стратегию второго игрока. Теорема доказана.

Следствие. Поскольку смешанная стратегия первого игрока остается в S-игре той же самой, что и в обычной игре, из доказанной теоремы следует, что S – игра полностью эквивалентна обычной игре, т.е. любая игра может быть представлена в виде эквивалентной S-игры.

 

Дальше будем обозначать S-игру через . Для перехода от игры к S-игре вместо пространства смешанных стратегий второго игрока необходимо использовать пространство S-стратегий, т.е. выпуклую оболочку . Обозначим потери второго игрока в S-игре через , тогда S — игра зависит от P, и , причем потери должны быть найдены на скалярном произведении . Таким образом выражение определяет S-игру. Функция потерь определяется выражением:

.

Рассмотрим процедуру оценки верхних и нижних цен в S-игре. Если первый игрок применяет смешанную стратегию , то значение его гарантированного выигрыша

.

Обозначим через такую стратегию первого игрока, при которой достигает максимума:

(эта нижняя цена игры совпадает с ценой игры в обычной форме в силу эквивалентности S-игры с обычной игрой). Стратегию называют максиминной стратегией первого игрока.

Предположим теперь, что второй игрок применяет некоторую стратегию . При этом значение его проигрыша . Тогда второго игрока будет интересовать стратегия:

. Стратегию называют минимаксной стратегией второго игрока.

Таким образом, максиминная стратегия первого игрока определяет нижнюю цену в S-игре:

.

Аналогично стратегия определяет верхнюю цену в S-игре:

.

Выражения для и можно представить в более удобном виде, если воспользоваться теоремой.

Теорема. Если S — произвольная точка m-мерного пространства и — многомерная переменная, то имеет место соотношение

.

Доказательство. Пусть . Рассмотрим частное значение p, соответствующее случаю

при и при . В этом случае . Таким образом, является частным значением скалярного произведения , а значит, подмножеством множества значений , получающихся при всевозможных значениях p. На основании теоремы о верхней границе подмножества находим

.

С другой стороны, заменяя в выражении для значения на максимальное значение , получаем

.

Это выражение справедливо при любом p. Сопоставляя два последних выражения приходим к соотношению:

. Теорема доказана.

Если воспользоваться доказанной теоремой, то выражение для B(S) можно переписать в виде

.

Из этого равенства вытекают два следствия:

1. , т.е. любая точка имеет по крайней мере одну координату, не меньшую, чем верхняя цена игры;

2. Если в качестве S взять , то получим:

. Верхняя цена игры равна максимальной из координат точки , определяющей минимаксную стратегию второго игрока.