Принятие решений в условиях определенности

Тема 2

Принятие решений у задачах исследования операций

1. Типичные классы задач исследования операций на транспорте

Накопленный опыт в решении практических задач исследования операций и его систематизация позволяют выделить по содержательной постановке следующие типичные классы задач: 1) управления запасами, 2) распределения ресурсов, 3) ремонта и замены оборудования, 4) массового обслуживания, 5) упорядочения, 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные.

Рассмотрим краткие особенности каждого класса задач.

Задачи управления запасами составляют самый распространенный и изученный в настоящее время класс задач исследования операций. Они обладают следующей особенностью. С увеличением запасов увеличиваются расходы на их хранение, но уменьшаются потери из-за возможной их нехватки. Следовательно, одна из задач управления запасами заключается в определении такого уровня запасов, который минимизирует следующий критерий: сумму ожидаемых затрат по хранению запасов, а также потерь из-за их дефицита.

В зависимости от условий задачи управления запасами делятся на следующие три группы:

1. Моменты поставок или оформления заказов на пополнение запасов фиксированы. Определить объемы производимых или закупаемых партий запасов.

2. Объемы производимых или закупаемых партий запасов фиксированы. Определить моменты оформления заказов на поставки.

3. Моменты оформления заказов и объемы производимых или за­купаемых партий не фиксированы. Определить эти величины, исходя из сформулированного выше критерия.

Задачи распределения ресурсов возникают, когда существует определенный набор работ (операций), которые необходимо выполнять, а наличных ресурсов для выполнения каждой работы наилучшим образом, не хватает.

В зависимости от условий задачи распределения ресурсов делятся на три группы:

1. Заданы и работы, и ресурсы. Распределить ресурсы между работами таким образом, чтобы максимизировать некоторую меру эффективности (прибыль) или минимизировать ожидаемые затраты (издержки производства).

Пример 1.1. Известны производственное задание и производственные мощности предприятия. При существующих различных способах получения изделий (например, обработка на разных станках) ограничение по мощности не позволяет для каждого изделия использовать наилучшую технологию.

Какие способы производства надо выбрать для каждого вида изделий, чтобы выполнить задание с минимальными затратами?

2. Заданы только наличные ресурсы. Определить, какой состав работ можно выполнить с учетом этих ресурсов, чтобы обеспечить максимум некоторой меры эффективности.

Пример 1.2. Задано предприятие с определенными производственными мощностями. Какую продукцию следует производить, чтобы получить максимальный доход?

3. Заданы только работы. Определить, какие ресурсы необходимы для того, чтобы минимизировать суммарные издержки производства.

Пример 1.3. Известно месячное расписание движения пассажирских самолетов по авиалиниям. Какое количество экипажей необходимо подобрать, чтобы выполнить план перевозок с минимальными эксплуатационными затратами?

Задачи ремонта и замены оборудования появляются в тех случаях, когда работающее оборудование изнашивается, устаревает и со временем подлежит замене.

Изношенное оборудование подвергают либо предупредительно-восстановительному ремонту, улучшающему его технологические характеристики, либо полной замене. При этом возможная постановка задачи такова.

Определить такие сроки восстановительного ремонта и момент замены оборудования модернизированным, при которых минимизируется сумма затрат на ремонт и замену оборудования при его старении за все время эксплуатации.

Существует и такое оборудование, в котором детали полностью выходят из строя, не восстанавливаются и подлежат замене (например, перегоревшие электронные лампы). Постановка задачи в этом случае следующая.

Определить такие сроки профилактического контроля по обнаружению неисправностей, при которых минимизируется сумма затрат на проведение контроля и ожидаемых потерь от простоя оборудования, вследствие выхода из строя деталей в интервале между соседними проверками (контролем).

Задачи массового обслуживанияпосвящены изучению и анализу систем обслуживания с очередями заявок, или требований. С явлением образования очередей приходится сталкиваться как в производственной практике, так и в быту. Типичными примерами являются очереди самолетов, ожидающих взлета или посадки, очереди клиентов в ателье бытового обслуживания, абонентов, ожидающих вызова на междугородной АТС, и т. д.

Очереди возникают из-за того, что поток требований или клиентов на обслуживание неуправляем и случаен. Если количество приборов обслуживания (взлетно-посадочные полосы аэродрома, приемщики в ателье бытового обслуживания, каналы связи и т. д.) достаточно велико, то очередь образуется редко, однако неизбежны длительные простои оборудования. С другой стороны, при малом количестве приборов создается значительная очередь и будут большие потери из-за, ожидания в очереди. Поэтому возможна следующая постановка задач массового обслуживания. Определить, какое количество приборов обслуживания необходимо, чтобы минимизировать, суммарные ожидаемые потери от несвоевременного обслуживания и простоев оборудования.

Задачи упорядоченияхарактеризуются следующими особенностями. Например, имеется множество различных деталей с определенными технологическими маршрутами, а также несколько единиц оборудования (фрезерный, токарный и строгальный станки), на которых эти детали обрабатываются. Так как одновременно обрабатывать более одной детали на одном станке невозможно, у некоторых из станков может образоваться очередь работ, т. е. деталей, ждущих обработки. Время обработки каждой детали известно. Определить такую очередность обработки деталей на каждом станке, при которой минимизируется некоторый критерий оптимальности, например, суммарная продолжительность завершения комплекса работ. Такая задача называется задачей календарного планирования или составления расписания, а выбор очередности запуска деталей в обработку — упорядочением.

Критерии оптимальности, используемые в задачах календарного планирования, имеют различный вид. Наиболее часто встречаются следующие критерии:

1. Минимизация общей продолжительности работ, т. е. интервала времени между моментом начала первой операции и моментом окончания последней.

2. Минимизация общего запаздывания. Запаздывание определяется как разность между фактическим и директивным сроком завершения обработки по каждой детали. Общее запаздывание представляет собой сумму запаздываний по всем деталям.

3. Минимизация максимального запаздывания, т. е. минимизация запаздывания по той детали, для которой эта величина является наибольшей.

4. Минимизация потерь, обусловленных запаздыванием.

Задачи сетевого планирования и управления (СПУ).В этом классе задач рассматривается соотношение между сроком окончания крупного комплекса операций и моментами начала всех операций комплекса. Они актуальны при разработке сложных и дорогостоящих проектов.

Для строгой постановки задач необходимы такие условия:

должно существовать точно определяемое множество операций, которые надо выполнить для завершения всего комплекса, включающего эти операции в качестве своих элементов;

множество операций комплекса упорядочено так, что для каждой операции известно, какие операции непосредственно ей предшествуют, а какие следуют за ней;

в пределах заданного отношения упорядочения операции можно начинать и заканчивать независимо друг от друга;

известна взаимосвязь между величиной потребляемого ресурса и длительностью каждой операции.

Комплекс операций в этом случае можно представить в виде сетевого графика, состоящего из вершин (узлов) и ориентированных дуг. В этом случае операции изображают дугами, а вершины представляют собой некоторые события. Дуги, входящие в вершину, отвечают операциям, которые должны быть закончены раньше, чем можно будет начать операции, изображенные исходящими дугами. Событию, соответствующему началу выполнения комплекса, присваивают номер 0. Остальные события нумеруют так, что, если события і, j связаны некоторой операцией (і, j), то выполняется неравенство t_a (j) >• t_в (і) + t_ij, где t_а (і), t_в(j) — моменты наступления событий і, j и t_ij — длительность операции (i, j). Если выполняются вышеизложенные условия и допущения, возможны следующие постановки задач сетевого планирования и управления.

1. Задана продолжительность всего комплекса. Определить сроки начала каждой операции, при которых минимизируется один из следующих критериев: а) общие затраты на выполнение всего комплекса работ; б) среднеквадратичный показатель неравномерности потребляемых ресурсов; в) вероятность невыполнения комплекса работ в директивный срок; г) среднеквадратичное отклонение требуемых ресурсов от наличных.

2. Заданы общие ресурсы. Определить сроки начала каждой операции, при которых минимизируется продолжительность выполнения всего комплекса работ. Методы решения задач СПУ изложены в [11].

Задачи выбора маршрута,или сетевые задачи чаще всего встречаются при исследовании разнообразных процессов на транспорте и в системах связи. Типичной задачей является задача нахождения некоторого маршрута проезда из города А в город В при наличии нескольких маршрутов для разных промежуточных пунктов. Стоимость проезда и затрачиваемое на проезд время зависят от выбранного маршрута. Определить наиболее экономичный маршрут по выбранному критерию оптимальности.

На допустимые маршруты может быть наложен ряд ограничений. Так, вводят запрет на возврат к уже пройденному пункту (узлу сети) или требование обхода всех пунктов сети с условием, что в каждом пункте можно побывать только один раз (задача коммивояжера).

В пунктах сети возможны задержки (например, на перекрестках шоссейных дорог). Эти задержки зависят от нагрузки на узел, занятости исходящих коммуникаций, ограниченной пропускной способности пунктов сети или носят случайный характер.

Среди сетевых задач наиболее распространенными являются задача выбора кратчайшего пути между произвольными пунктами сети, задача коммивояжера, задача о максимальном потоке [1].

Комбинированные задачи включают в себя несколько типовых моделей задач одновременно. Например, при планировании и управлении производством приходится решать следующий комплекс задач:

1) сколько изделий каждого типа необходимо выпустить и каковы оптимальные размеры партий изделий? (Типичная задача планирования производства);

2) распределить производственные заказы по видам оборудования после того как определен оптимальный план производства. (Типичная задача распределения);

3) в какой последовательности и когда следует выполнять производственные заказы? (Типичная задача календарного планирования).

Так как эти три задачи нельзя решить изолированно, независимо друг от друга, то возможен следующий подход к решению данной комбинированной задачи. Сначала получают оптимальное решение задачи планирования производства. Затем в зависимости от этого оптимума находят наилучшее распределение оборудования. Наконец, на основе такого распределения составляют оптимальный график выполнения работ.

Однако такая последовательная оптимизация частных подзадач не всегда приводит к оптимальному решению задачи в целом. В частности, например, может оказаться, что нельзя произвести все изделия в оптимальных количествах из-за ограниченности имеющихся ресурсов. Пока еще не найден метод, позволяющий получить одновременный оптимум для всех трех задач, а возможно он не существует для конкретных задач. Поэтому для решения подобных комбинированных задач применяется метод последовательных приближений, позволяющий приблизиться к искомому решению комбинированной задачи достаточно близко [1, 49].

Предложенная классификация задач исследования операций не является окончательной. Со временем некоторые классы задач объединяются и становится возможным их совместное решение, стираются границы между указанными классами задач, а также появляются новые классы задач.

Некоторые принципы принятия решении в задачах исследования операций

Теория принятия решений является фундаментом науки исследования операций. В процессе принятия решений возникают такие трудности:

1. Большое число критериев, которые не всегда согласованы между собой. Например, при проектировании нового устройства часто выдвигается требование максимальной надежности и минимальной стоимости изделия. Эти критерии являются противоречивыми, поэтому возникает задача компромисса между ними;

2. Высокая степень неопределенности, которая обусловлена недостаточной информацией для обоснованного принятия решений.

 

Элементы процесса принятия решений и классификация задач

Любой процесс принятия решений включает следующие элементы:

1. Цель. Необходимость принятия решений определяется целью или несколькими целями, которые должны быть достигнуты.

2. Лицо, принимающее решение, должно нести ответственность за последствия этих решений.

3. Альтернативные решения (различные варианты достижения целей).

4. Внешняя среда (совокупность всех внешних факторов, влияю­щих на исход решения).

5. Исходы решений.

6. Правила выбора решений (решающие правила).

Эти правила позволяют определить наиболее предпочтительное в смысле выбранного критерия решение.

Решающее правило отражает информированность лица, принимающего решение, о возможных исходах выбранных решений, а также предпочтительность тех или иных исходов. Итак, основой для построения решающих правил служит информация о предпочтении различных альтернатив для лица, принимающего эти решения.

Теория принятия решений использует различные процедуры, позволяющие формализовать предпочтения, т. е. выразить их в единой количественной мере. Основой для таких процедур является теория полезности, разработанная Дж. фон Нейманом и О. Моргенштерном 135]. Ее математическая основа — система аксиом, в которых утверждается, что существует некоторая мера ценности, позволяющая упорядочить результаты решений. Эта мера называется функцией полезности решений или полезностью [43].

В зависимости от условий внешней среды и степени информированности лица существует следующая классификация задач принятия решений: а) в условиях определенности, б) в условиях риска, в) в условиях неопределенности, г) в условиях конфликтных ситуаций или противодействия (активного противника).

 

Принятие решений в условиях определенности характеризуется однозначной или детерминированной связью между принятым решением и его исходом. Основная трудность — наличие нескольких критериев, по которым следует сравнивать исходы.

Здесь возникает задача принятия решений при так называемом «векторном критерии» [12].

Случай 1. Пусть имеется совокупность критериев:

Найти решение, которое окажется наилучшим в смысле выбираемого критерия.

Если все критерии измеряются в одной шкале, то обобщенный критерий F₀ (x) можно записать в виде взвешенной суммы этих критериев

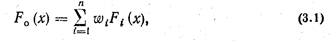
где w_{ — вес соответствующего критерия.

В этом случае необходимо найти max F₀ (x).

Если же эти критерии измеряются в различных шкалах, то необ­ходимо привести их к одной шкале. Для этого формируют критерий

где

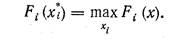
Следовательно, требуется свести к минимуму величину уклонения каждого критерия от его максимального значения.

При таком формировании обобщенного критерия возникает некоторое несоответствие, связанное с тем, что можно добиться высоких показателей по одним критериям за счет ухудшения показателей по другим. В этом случае значения некоторых частных критериев могут оказаться меньше предельно допустимых значений Fi (х) < Fi _лоп.

Однако часто необходимо, чтобы выполнялось следующее условие:

Поэтому можно предложить

еще один способ образования обобщенного критерия.

Допустим, что по каждому критерию определены предельные значения F_{i доп}, i = 1, n.

Если условие (3.3) выполняется, то можно принять f_i (х) равным его собственному значению.

Если это условие не выполняется, то нужно принять Fi (х) = — ∞.

 

В таком случае задача сводится к нахождению

при условии (3.3).

Случай 2. Предположим, что критерии упорядочены в последовательности F₁, F₂, ..., F_n.

Тогда задача отыскания оптимального решения может быть записана как

(3.5)

при ограничениях:

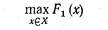
Два варианта логического объединения критериев. Предположим, что критерии F₁, F₂, ..., F_n могут принимать только два значения 0 или 1.

F_i (x) = 1, если i-ая цель достигнута. В противном случае F_t (x) = 0.

Тогда обобщенный критерий может быть записан:

а) в виде конъюнкции критериев F_i, если общая цель операции состоит в выполнении всех целей одновременно, т. е.

б) в виде дизъюнкции критериев, когда общая цель операции достигается, если достигается хотя бы одна частная цель, т. е.

Методика определения полезности. Для принятия решений необходимо установить предпочтительность различных критериев (меру полезности тех или иных исходов) для Лица, принимающего решение.

Методика определения полезности возможных результатов разработана в [1].

Практическое применение теории полезности основывается на сле­дующих аксиомах [43]:

1) Результат x_i оказывается предпочтительнее х_j (это записывается так: х_i > x_j), тогда и только тогда, когда и (х_i) > и (х_j), где и (х_i) и и (х_j) — полезности результатов х_i и х_j соответственно.

2) Транзитивность: если x_i > х_j, а х_j > x_k, то и (x_i) > и (x_k).

3) Линейность: если некоторый результат х представлен в виде х = (1 - k) x₁ + +kх₂ где 0 < k < 1, то и (х) = (1 — k) и (х ₁) + ku (x₂).

4) Аддитивность: если и (х_1, x₂ — полезность от достижения одновременно результатов х₁ и х₂, то свойство аддитивности следующее: и (х₁, х₂) = и (х₁) + и (х₂). Аналогично, если имеется п результатов, х₁, х₂, ..., х_п, достигаемых одновременно, то

Рассмотрим несколько вариантов методики определения полезности в различных случаях.

I. Случай, когда имеются два результата.

Методика определения полезности такова:

1. Определяем, какой результат более предпочтителен для лица, принимающего решение. Пусть x₁ > х₂, т. е. х₁ предпочтительнее, чем х₂.

2. Затем определяем такую вероятность α, при которой достижение результата х₁ будет эквивалентно результату х₂, получаемому с вероятностью 1.

Таблица 1.1

 

3. Оцениваем соотношение между полезностями результатов х₁ и х₂. Для этого примем полезность

Тогда

II. Случай, когда имеются п возможных результатов х₁ х₂, ..., х_п, между которыми установлено отношение предпочтения х₁ > х₂ > > х₃ > ... > х_п.

Для этого случая методика определения полезности следующая:

1. Определяем величину α₁ из условия

2. Аналогично определяем

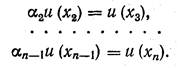
3. Положив полезность наименее предпочтительного результата х_n равной единице, находим

III. Случай, когда некоторые критерии являются качественными. Применяется методика, основанная на алгоритме, предложенном Р. Акофом и Р. Черчменом [1].

Предположим, что имеется п результате» х₁, х₂, …, х_п. Методика определения полезности состоит из следующих этапов:

1. Упорядочивают все результаты по убыванию предпочтительности. Пусть х₁ — наиболее, а х_n — наименее предпочтительный результат.

Составляют таблицу возможных комбинации результатов, достигаемых одновременно, и затем устанавливает их предпочтение относительно отдельных результатов х₁, х₂, ..., х_n (табл. 1.1).

Эту информацию о предпочтительности результатов получают от экспертов.

2. Приписывают начальные оценки полезностям отдельных результатов и₀(х₁). и₀(х₂), .... и₀(х_n). Затем подставляют начальные оценки в последнее соотношение табл. 1.1. Если оно удовлетворяется, то оценки не изменяют.

В противном случае производят коррекцию полезностей так, чтобы удовлетворялось данное соотношение.

3. После этого переходят к следующему соотношению. Процесс коррекции продолжается до тех пор, пока не образуется система оценок и* (x₁), и* (х₂), .... и* (х_n), которая будет удовлетворять всем указанным в таблице соотношениям. Коррекцию следует производить таким образом, чтобы по возможности изменять оценки для минимального количества результатов.

Пример 1.4. Пусть эксперт упорядочивает пять результатов х₁,х₂,…,х₅, приписав им следующие оценки: и₀ (х₁) = 7; и₀ (x_z) = 4; u_a (х₃) = 2 и₀ (х₄) = 1,5 и_о (х₅) = 1.

Рассмотрев возможные варианты выбора, он высказал следующее суждение относительно ценности тех или иных комбинаций результатов.

1) х₁ < х₂ + х₃ + х₄ + х₅,

2) х₁<х₂ + х₃ + х₄,

3) х₁ < х₂ + х₃ + х_5,

4) х₁>х₂ + х₂,

5) x₂<x_a+x_t + Xi,

6) х₂ > х₃ + х4,

7) х₃ > х₄ + х₅.

Нужно произвести оценку полезности результатов, так чтобы удовлетворить всем неравенствам.

Подставляем начальные оценки в неравенство 7):

Следовательно, неравенство 7) не удовлетворяется.

Изменяем полезность результата х₃ и проверяем неравенство 6):

Это неравенство также не удовлетворяется.

Примем и₁ (х₂) = 5. При этом неравенство 5) удовлетворяется.

Обращаемся к неравенству 4);

Оно не выполняется.

Поэтому

примем и₁(x₁) — 8,5. Теперь неравенства 3), 2), 1) удовлетворяются.

Проверяем еще раз неравенства 6) и 7) при измененных значениях полезностей: 5 > 3 + 1,5 и 3 > 1,5+ 1. Оба неравенства выполняются.

Выпишем окончательные оценки полезности результатов: u₁ (х₁) = 8,5; и₁ (х₂) = 5; и₁ (х2) = 3; u₁ (х₄) = 1,5; и₁ (x₅) = 1.

Такая методика определения полезности применима, когда коли­чество результатов п ограничено п < 6—7.

В случаях, когда п > 7, авторами предложена следующая моди­фикация данной методики — способ коррекции оценок [1].

Множество результатов разбивают на подмножества, состоящие из 5—7 результатов и имеющие один общий результат, например, х₁. Затем приписывают начальные значения полезностям для всех результатов, причем полезность общего результата х₁ одинакова во всех подмножествах. Далее применяют способ коррекции оценок полезности независимо в каждом из подмножеств с ограничением и (х₁) = const. В результате получают систему полезностей с единой мерой для всех подмножеств и (х_i).