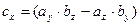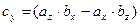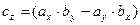Статика. Введение.
Введение
Теоретическая механика – это наука в которой изучаются механические движения вещественных форм материальных объектов.
Теоретическую механику называют еще классической механикой или механикой Ньютона.
Механическое движение – это перемещение материальных объектов в пространстве с течением времени без рассмотрения физических свойств этих объектов и их изменения в процессе движения.
Теоретическая механика изучает только вещественные формы материальных объектов. Элементарные частицы и различные поля не являются предметом изучения в теоретической механике.
Движение материальных объектов происходит в пространстве и во времени. Пространство является трехмерным пространством Эвклида.
Теоретическая механика является базой для других разделов механики (теории упругости, сопротивления материалов, теории механизмов и машин и пр.) и многих технических дисциплин.
Теоретическая механика делится на три части: статику, кинематику и динамику. Главной частью является динамика.
Изучение теоретической механики обычно начинается со статики.
Рекомендуемая литература:
1. В.В.Добронравов, Н.Н.Никитин «Курс теоретической механики». М., Высшая школа, 1974 г. и последующие издания.
2. С.М.Тарг. «Краткий курс теоретической механики». М., Высшая школа, 2001 г.
3. А.А.Яблонский. «Курс теоретической механики». М., Высшая школа 1977 г. и последующие издания.
4. Г. Корн и Т. Корн. СПРАВОЧНИК ПО МАТЕМАТИКЕ. Для научных работников и инженеров. М., «Наука», 1970
Статика - это раздел теоретической механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил.
Под равновесием тела в статике понимается состояние его покоя по отношению к другим телам, принимаемым за неподвижные.
Элементы векторной алгебры
В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.
1. Понятие вектора.
Для определенности рассматриваем прямоугольную декартову систему координат.
Вектор это направленный отрезок, который характеризуется длиной и направлением.
Операции над векторами. Вектора можно складывать и умножать на число.
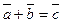 сумма двух векторов есть вектор
сумма двух векторов есть вектор
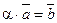 произведение вектора на действительное число есть вектор
произведение вектора на действительное число есть вектор
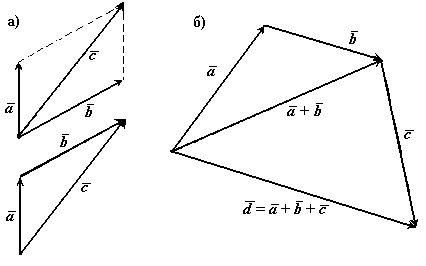 |
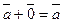 существует нулевой вектор
существует нулевой вектор
Рис. 1-1
В математике все вектора являются свободными, их можно переносить параллельно самим себе.
В сумме двух векторов (рис. 1-1а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис. 1-1б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.
Операции над векторами подчиняются следующим законам (см. рис. 1-2):



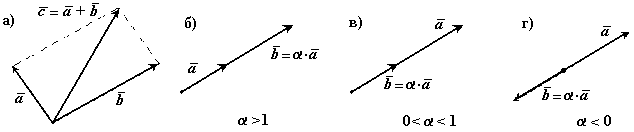
Рис. 1-2
2. Правые и левые системы координат.
Декартовы системы координат делятся на два вида: правую и левую.
Рассмотрим декартовы системы координат на плоскости (см. рис. 1-3).
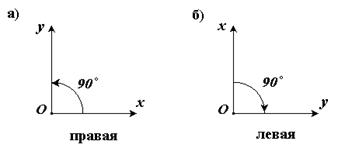 |  | ||
При повороте оси Ox правой системы координат на 90о против часовой стрелки она совпадает с осью Oy .
Рис. 1-3 Рис. 1-4
Рассмотрим декартовы системы координат в пространстве (см. рис. 1-4).
При повороте оси Ox правой системы координат вокруг оси Oz на 90о против часовой стрелки она совпадает с осью Oy .
3. Длина, проекции и направляющие косинусы вектора.
В дальнейшем будем рассматривать правую декартову систему координат. Единичные вектора вдоль осей Ox, Oy и Oz образуют систему единичных (или базисных) векторов. Любой вектор, имеющий начало в точке O, можно представить как сумму 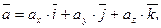 числа (ax , ay , az ) - это проекции вектора
числа (ax , ay , az ) - это проекции вектора 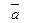 на оси координат (см. рис. 1-5).
на оси координат (см. рис. 1-5).
Длина (или модуль) вектора 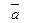 определяется формулой
определяется формулой 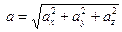 и обозначается
и обозначается  или
или 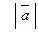
Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис. 1-6).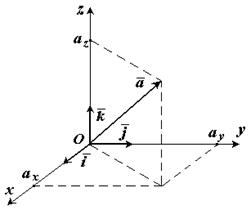

Рис. 1-5
Рис. 1-6
Направляющими косинусами cos(a), cos(b), cos(g) вектора называются косинусы углов между вектором и положительными направлениями осей Ox, Oy и Oz соответственно.
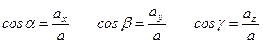
Любая точка пространства с координатами (x, y, z) может быть задана своим радиус-вектором
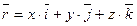
Координаты (x, y, z) это проекции вектора 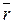 на оси координат.
на оси координат.
4. Скалярное произведение двух векторов
Имеется два вектора 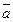 и
и 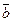 .
. 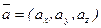 ,
, 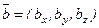 .
.
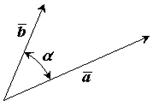 Результатом скалярного произведения двух векторов
Результатом скалярного произведения двух векторов 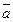 и
и 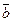 является скалярная величина (число).
является скалярная величина (число).
Записывается как 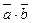 или
или 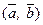 . Скалярное произведение двух векторов равно
. Скалярное произведение двух векторов равно 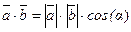
Рис. 1-7
Свойства скалярного произведения:

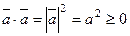

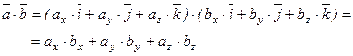
5. Векторное произведение двух векторов
Имеется два вектора 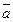 и
и 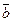 .
. 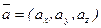 ,
, 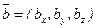 .
.
 Результатом векторного произведения двух векторов
Результатом векторного произведения двух векторов 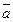 и
и 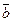 является вектор
является вектор 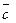 . Записывается как
. Записывается как 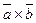 или
или 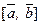 .
.
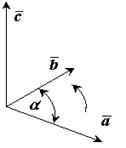
Векторное произведение двух векторов это вектор 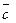 , перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора
, перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора 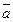 к вектору
к вектору 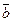 был виден против часовой стрелки.
был виден против часовой стрелки.
Рис. 1-8
Длина (или модуль) векторного произведения равна 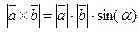 .
.
Свойства векторного произведения:

Векторное произведение двух векторов вычисляется через их проекции следующим образом: