Главный момент системы сил

Определение. Главным моментом системы сил относительно полюса 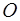называется геометрическая сумма моментов всех сил системы относительно этого полюса.

Обозначение: , или . Если задана система сил , то

.

Определение. Главным моментом системы сил относительно оси называется алгебраическая сумма моментов всех сил системы относительно этой оси.

Обозначение: , или

.

Теорема. Проекция главного момента системы сил относительно полюса 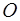на ось , проходящую через этот полюс, равна главному моменту сил системы относительно этой оси, то есть

.

Доказательство:

Главный момент системы сил относительно полюса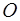

.

Спроектируем это векторное равенство на ось , проходящую через полюс :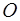

.

На основании теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси

.

Следовательно .

4.6. Зависимость между главными моментами системы сил относительно двух полюсов

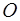Дана система сил и два полюса: старый и новый (рис. 23).

Главный момент системы сил относительно старого полюса:

.

Главный момент относительно нового полюса:

.

Здесь и ()–радиус-векторы точки приложения силы относительно старого и нового полюсов соответственно.

Из рисунка видно, что:

.

Тогда

,

где 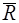–главный вектор. Пришли к теореме о зависимости между главными моментами системы сил относительно двух полюсов.

Теорема. Главный момент системы сил относительно нового полюса равен сумме главного момента системы сил относительно старого полюса и момента главного вектора, приложенного к старому полюсу относительно нового –полюса, то есть

.

Следствие 1. Если главный вектор системы сил равен нулю, то ее главный момент не зависит от выбора полюса, то есть, если , то .

Следствие 2. Главный момент пары сил не зависит от выбора полюса и отличен от нуля.

Дана пара сил {} (рис. 24). , . Так как главный вектор . То главный момент пары не зависит от выбора полюса:

.

 

 

Линия действия силы 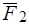проходит через полюс , то есть, и:

.