СИСТЕМА СХОДЯЩИХСЯ СИЛ

 

Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке – центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими.

Рассмотрим общий случай пространственной системы сходящихся сил.

Применяя к первым двум силам пучка и аксиому параллелограмма, заменим их одной равнодействующей силой

.

Затем по правилу параллелограмма складываем силы и получаем их равнодействующую:

и т. д. Продолжая процесс векторного сложения сил для всех n сил, получим

Таким образом, система n сходящихся сил эквивалентна одной силе , которая и является равнодействующей этой системы сил.

Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. (рис. 5)

 

Итак, система сходящихся сил в общем случае приводится к одной силе - равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы.

Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.

.

; ; .

По проекциям определяем модуль равнодействующей силы

 

и косинусы углов ее с осями координат по формулам:

 

; ;

 

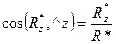
Условия равновесия системы сходящихся сил

 

Условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. (рис. 6)

Условия равновесия пространственной системы сходящихся сил в аналитической форме:

; ; ,

т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.

; ,

т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.