Построение планов скоростей и ускорений
Лекция № 3
Планом скоростей (ускорений) называют рисунок, на котором в масштабе изображены векторы, равные по модулю и направлению скоростям (ускорениям) различных точек механизма в данный момент времени.
Планы скоростей и ускорений строятся по векторным уравнениям, которые составляются отдельно для каждой группы Ассура в порядке присоединения их к ведущему звену и к другим звеньям механизма.
Построение планов скоростей и ускорений рассмотрим на примере шарнирного четырехзвенника (рис.1, а).
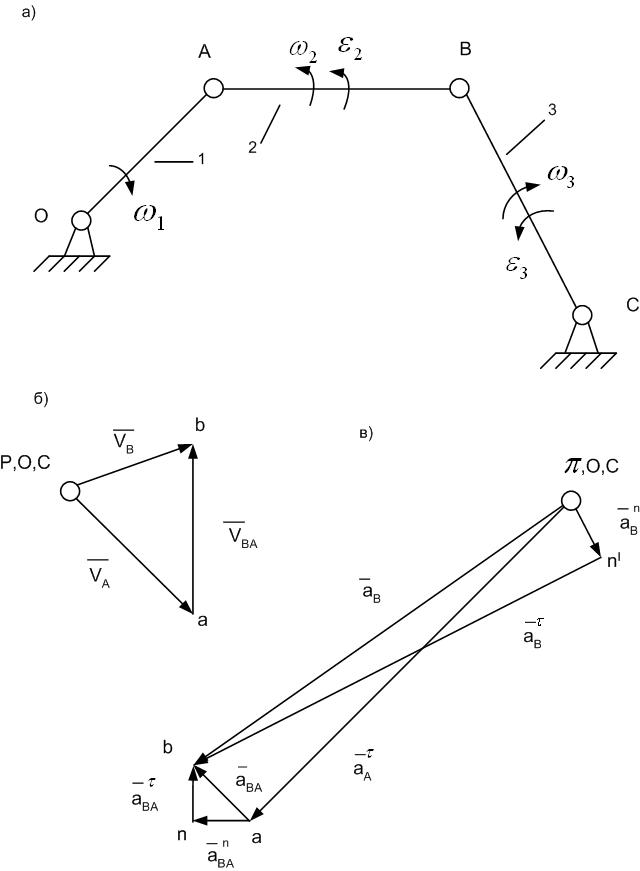
Рис. 1. Построение планов скоростей и ускорений для шарнирного четырехзвенного механизма
Известными являются:
а) размеры звеньев 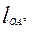
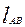 ,
, 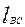 ,
, 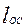 ;
;
б) положение механизма;
в) закон движения ведущего звена 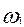 .
.
Построение планов ведется в порядке построения механизма.
Для ведущего звена определяем величину скорости в точке 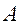 :
:
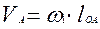 . (3.1)
. (3.1)
Вектор 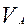 перпендикулярен радиусу, т.е. отрезку
перпендикулярен радиусу, т.е. отрезку 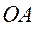 , и направлен в сторону, определяемую направлением
, и направлен в сторону, определяемую направлением 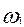 .
.
Задаемся масштабом плана скоростей 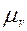 и вычисляем отрезок
и вычисляем отрезок 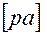 , изображающий в выбранном масштабе вектор
, изображающий в выбранном масштабе вектор 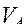 ,
,
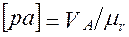 .
.
Из произвольной точки  , называемой полюсом плана скоростей, откладываем в указанном направлении отрезок
, называемой полюсом плана скоростей, откладываем в указанном направлении отрезок 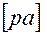 (рис. 1, б).
(рис. 1, б).
Составим векторные уравнения для группы Ассура 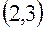 . Точка
. Точка  принадлежит звеньям
принадлежит звеньям 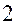 и
и 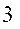 , поэтому
, поэтому
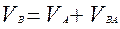 , (3.2)
, (3.2)
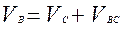 .(3.3)
.(3.3)
В нашем случае уравнение (3.2) превращается в тождество, т.к. скорость точки 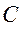 равна нулю
равна нулю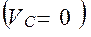 , поэтому обходимся одним уравнением (3.2).
, поэтому обходимся одним уравнением (3.2).
Скорость точки  известна по направлению: так как точка
известна по направлению: так как точка  движется по окружности радиусом
движется по окружности радиусом 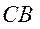 , то она перпендикулярна радиусу –
, то она перпендикулярна радиусу –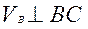 , величина ее нам неизвестна. Скорость точки
, величина ее нам неизвестна. Скорость точки  относительно точки
относительно точки 
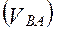 также известна по направлению –
также известна по направлению – 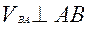 . Величина ее нам неизвестна.
. Величина ее нам неизвестна.
Решая векторное уравнение графическим способом, получим план скоростей, т.к. векторное уравнение эквивалентно двум скалярным уравнениям.
В соответствии с векторным уравнением (3.2) через конец вектора 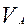 (точку
(точку  ) проводим направление вектора
) проводим направление вектора 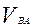
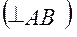 , а через полюс
, а через полюс  – направление вектора
– направление вектора 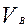
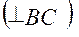 . Пересечение этих направлений (точка
. Пересечение этих направлений (точка 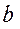 ) определяет отрезки
) определяет отрезки 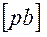 ] и
] и 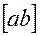 , изображающие в выбранном масштабе скорости соответственно
, изображающие в выбранном масштабе скорости соответственно 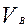 и
и 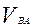 . Величины этих скоростей равны:
. Величины этих скоростей равны:
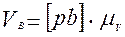 ;
;
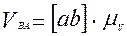 .
.
Пользуясь построенным планом скоростей, можно определить угловые скорости звеньев 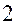 и
и 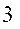 :
:
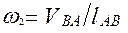 ;
;
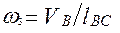 .
.
Для определения направления 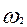 переносим вектор
переносим вектор 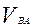 в точку
в точку  механизма и рассматриваем движение этой точки относительно точки
механизма и рассматриваем движение этой точки относительно точки 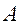 по направлению скорости
по направлению скорости 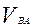 . Из рисунка видно, что
. Из рисунка видно, что 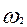 направлена против часовой стрелки.
направлена против часовой стрелки.
Аналогично определяем направление угловой скорости 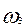 . Перенеся вектор
. Перенеся вектор 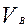 в точку
в точку , видно, что
, видно, что 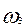 направлена по часовой стрелке.
направлена по часовой стрелке.
Построим план ускорений. Ускорение точки 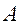 состоит только из нормального ускорения, т.к. звено
состоит только из нормального ускорения, т.к. звено 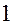 движется равномерно и оно равно
движется равномерно и оно равно

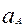 =
= 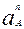
 =
= 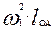 (3.4)
(3.4)
Вектор 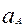 направлен по радиусу к центру – от точки
направлен по радиусу к центру – от точки  к точке
к точке  .
.
Задаемся масштабом плана ускорений 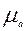 и вычисляем длину отрезка
и вычисляем длину отрезка 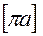 , изображающего вектор
, изображающего вектор 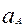 в этом масштабе.
в этом масштабе.
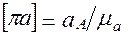 .
.
Из произвольной точки 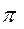 , называемой полюсом плана ускорений, в направлении вектора
, называемой полюсом плана ускорений, в направлении вектора 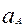 откладываем отрезок
откладываем отрезок 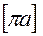 (рис.
(рис.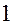 ,
,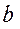 ).
).
Переходим к группе Ассура 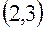 .
.
Векторные уравнения для точки  группы имеют вид:
группы имеют вид:
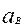 =
= 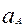 +
+  , (3.5)
, (3.5)
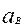 =
= 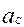 +
+ 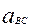 . (3.6)
. (3.6)
Так как точка 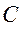 неподвижна, то ее ускорение равно нулю и уравнение (3.6) превращается в тождество. Поэтому можно ограничиться только уравнением (3.5).
неподвижна, то ее ускорение равно нулю и уравнение (3.6) превращается в тождество. Поэтому можно ограничиться только уравнением (3.5).
Ускорения 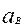 и
и  слагаются из нормальных и касательных составляющих:
слагаются из нормальных и касательных составляющих:
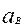 =
= 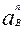 +
+ 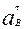 ,
,
 (3.7)
(3.7)
 =
= 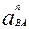 +
+ 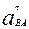 (3.8)
(3.8)
Подставляя значения 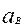 и
и  в уравнение (3.5), получим
в уравнение (3.5), получим
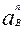 +
+ 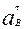 =
= 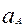 +
+ 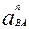 +
+ 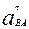 (3.9)
(3.9)
В уравнении (3.9) три вектора известны полностью – и по величине и по направлению, а два – только по направлению:
ускорение 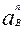 по величине равно
по величине равно
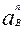 =
= 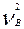 ¤
¤ 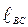 , (3.10)
, (3.10)
вектор 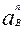 направлен вдоль звена
направлен вдоль звена  от точки
от точки  к точке
к точке  – оси вращения звена;
– оси вращения звена;
вектор 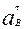 направлен перпендикулярно звену
направлен перпендикулярно звену  ;
;
ускорение 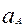 известно полностью;
известно полностью;
ускорение 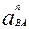 по величине равно
по величине равно

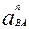 =
=  /
/  ,(3.11)
,(3.11)
направлен вектор 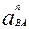 вдоль звена АВ от точки
вдоль звена АВ от точки  к точке
к точке 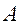 ;
;
вектор 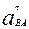 направлен перпендикулярно звену
направлен перпендикулярно звену  .
.
Построим план ускорений. Согласно правой части уравнения (3.9), из конца вектора 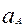 , (отрезка
, (отрезка 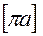 ) откладываем в масштабе в указанном выше направлении вектор
) откладываем в масштабе в указанном выше направлении вектор  , представляемый отрезком
, представляемый отрезком  , который вычисляется по формуле
, который вычисляется по формуле
 =
= 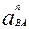 /
/  .
.
Из конца вектора 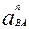 (точки
(точки  ) проводим направление вектора
) проводим направление вектора 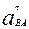 (
(
 ).
).
Согласно левой части уравнения (3.9) из полюса плана ускорений 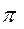 откладываем в указанном ранее направлении вектор
откладываем в указанном ранее направлении вектор 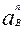 , изображаемый отрезком
, изображаемый отрезком  , который вычисляется по формуле
, который вычисляется по формуле
 =
= 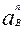 / mа .
/ mа .
Из конца вектора 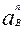 (точки
(точки ) проводим направление вектора
) проводим направление вектора 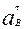 (^
(^  ). Пересечение направлений
). Пересечение направлений 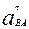 и
и 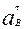 (точка
(точка  ) дает решение векторного уравнения: отрезок
) дает решение векторного уравнения: отрезок  изображает вектор
изображает вектор 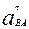 , а отрезок
, а отрезок  - вектор
- вектор 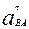 . Величины этих ускорений равны:
. Величины этих ускорений равны:
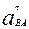 =
=  ×mа;
×mа; 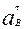 =
=  × mа.
× mа.
Складывая векторы 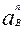 и
и 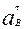 , т.е. соединяя точку
, т.е. соединяя точку 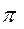 с точкой
с точкой 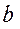 , получим отрезок
, получим отрезок  , который изображает вектор полного ускорения точки
, который изображает вектор полного ускорения точки  -
-  .
.
Складывая векторы 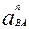 и
и 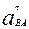 , т.е. соединяя точки
, т.е. соединяя точки  и
и 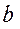 , получим отрезок
, получим отрезок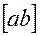 , который изображает вектор ускорения точки
, который изображает вектор ускорения точки 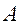 -
-  .
.
Величины этих ускорений равны:
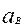 =
=  × mа;
× mа;  =
= 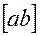 × mа.
× mа.
Определяем угловые ускорения звеньев 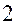 и
и 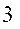 :
:
e2 = 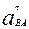 /
/  ; e3 =
; e3 = 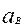 /
/ 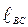 .(3.12)
.(3.12)
Для определения направления этих ускорений переносим векторы 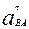 и
и 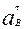 в точку
в точку  механизма. Рассматривая движение точки
механизма. Рассматривая движение точки  относительно точки
относительно точки 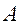 в направлении ускорения
в направлении ускорения 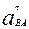 , устанавливаем, что e2 направлено против часовой стрелки. Рассматривая движение точки
, устанавливаем, что e2 направлено против часовой стрелки. Рассматривая движение точки  относительно точки
относительно точки 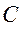 в направлении
в направлении 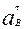 , устанавливаем, что e3 также направлено против часовой стрелки.
, устанавливаем, что e3 также направлено против часовой стрелки.
Векторы абсолютных скоростей и ускорений точек всегда направлены от полюса к данным точкам.
Векторы относительных скоростей и ускорений каких – либо точек всегда соединяют концы векторов соответствующих абсолютных скоростей и ускорений и также направлены к данной точке.