Координаты центров тяжести неоднородных тел.
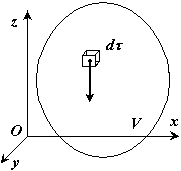
Рис.36
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.
Если оси х и у расположить в этой плоскости симметрии (рис.36), то для каждой точки с координатами 
можно отыскать точку с координатами 
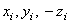. И координата 
по (2), будет равна нулю, т.к. в сумме 
все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Действительно, в этом случае, если ось z провести по оси симметрии, для каждой точки с координатами 
можно отыскать точку с координатами 
и координаты 
и 
, вычисленные по формулам (2), окажутся равными нулю.
Аналогично доказывается и третья теорема.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
И ещё несколько замечаний.
Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (2)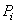 
– определять как вес соответствующей части и – как координаты её центра тяжести.
Второе. Если тело однородное, то вес отдельной части его 
, где 
- удельный вес материала, из которого сделано тело, а 
- объём этой части тела. И формулы (1) примут более удобный вид. Например,
И аналогично,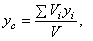 
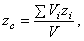где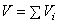 
- объём всего тела.
Третье замечание. Если тело состоит из однородных пластин одинаковой, малой толщины, то объём каждой пластины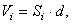 
где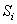 
– площадь пластины, d – толщина. И координаты центра тяжести будут определяться только с помощью площадей:
где 
– координаты центра тяжести отдельных пластин; 
– общая площадь тела.
Четвёртое замечание. Если тело состоит из стержней, прямых или криволинейных, однородных и постоянного сечения, то вес их 
где li – длина, 
– вес единицы длины (погонного метра), а координаты центра тяжести будут определяться с помощью длин отдельных участков:
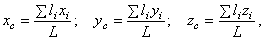
где 
– координаты центра тяжести 
-го участка; 
Отметим, что согласно определению центр тяжести - это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).
Координаты центра тяжести неоднородного твердого тела в выбранной системе отсчета определяются следующим образом:
где 
- вес единицы объема тела (удельный вес)
- вес всего тела.
Если твердое тело представляет собой неоднородную поверхность, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
где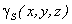 
- вес единицы площади тела,
- вес всего тела.
Если твердое тело представляет собой неоднородную линию, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
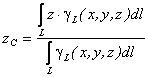
где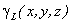
- вес единицы длины тела ,
- вес всего тела.