Равновесие при наличии трения.

Рис.27

Рис.26

 

Наиболь­ший угол 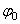, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения. Из чертежа видно, что

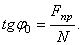
Так как 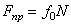, отсюда находим следующую связь между углом трения и коэффициентом трения:

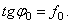
При равновесии полная реакцияR, в зависимости от сдвигающих сил, может проходить где угодно внутри угла трения. Когда равно­весие становится предельным, реакция будет отклонена от нормали на угол .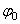

Конусом трения называют конус, описанный предельной силой реакции шероховатой связи 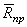вокруг направления нормальной реакции.

Если к телу, лежащему на шероховатой поверх­ности, приложить силуР, образующую угол 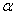с нор­малью (рис. 27), то тело сдвинется только тогда, когда сдвигающее усилие 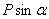будет больше 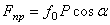(мы считаем 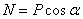, пренеб­регая весом тела). Но неравенство 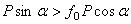, в котором 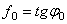, выполняется только при 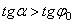, т.е. при 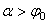. Следовательно, ни­какой силой, образующей с нормалью угол 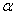, меньший угла трения 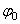, тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или само­торможения тел.

 

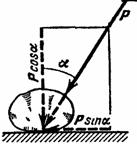
Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.

Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

 

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наиболь­шего значения 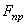. При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими N и 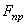, где 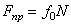. Затем составляют обычные условия равновесия статики, подставляют в них вместо 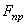величину 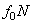и, решая полу­ченные уравнения, определяют искомые величины.

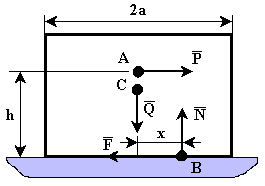
Пример 1.Рассмотрим тело, имеющее вертикальную плоскость симметрии (рис.28). Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2a.

К телу в точке С, лежащей на оси симметрии, приложена вертикальная сила 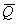и в точке А, лежащей на расстоянии 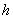от основания, горизонтальная сила 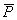. Реакция плоскости основания (реакция связи) приводится к нормальной реакции 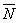и силе трения 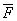. Линия действия силы 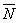неизвестна. Расстояние от точки С до линии действия силы 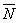обозначим x ().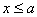