Движение точки задано, если известны координаты точки, как непрерывные, дважды дифференцируемые функции времени, т.е.

Движение точки можно изучать используя любую систему координат. Рассмотрим случай декартовой прямоугольной системы координат.

Координатный способ.

Векторный способ.

Будем рассматривать случай декартовой прямоугольной системы координат. Движение точки относительно рассматриваемой системы отсчета задано, если известен радиус-вектор этой точки как функция времени, т.е.

(1-1)

Векторный способ обычно применяется для теоретического изложения кинематики точки.

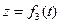, , (1-2)

Уравнения движения есть также уравнения траектории точки в параметрической форме. Параметром является время t.

(1-3)

Уравнения траектории в координатной форме получаются из уравнений (1-2) исключением параметра t. Получаются уравнения двух поверхностей , 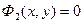. Пересечение этих поверхностей дает кривую в пространстве – траекторию точки.

 

Примеры:

Естественный способ задания движения.

При естественном способе задания движения задаются траектория точки и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы отсчета.

Для задания закона движения точки по траектории необходимо выбрать на траектории точку О, принимаемую за начало отсчета. Кроме того, необходимо задать начало отсчета времени.

Рис. 1.3

 

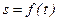- закон движения точки по траектории.

Функция 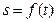должна быть непрерывной и дважды дифференцируемой.

От задания движения в декартовых координатах можно перейти к его заданию естественным способом. Закон движения точки по траектории в дифференциальной форме через декартовы координаты выражается в виде

и после интегрирования - в конечной форме

если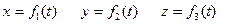

 

Примеры: