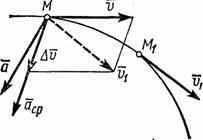
Вектор ускорения точки

Рис.3

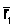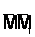в момент времени t в положении М, определяемом радиусом-векто­ром r, а в момент t₁ приходит в положение M₁ определяемое векто­ром (рис.3). Тогда перемещение точки за промежуток времени определяется вектором который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что ; следовательно, .

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую сред­ней по модулю и направлению скоростью точки за промежуток времени .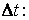

Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v_ср при стремлении промежутка времени к нулю:

, .

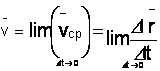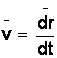Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

 

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и

направления скорости точки.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а

в момент t1 приходит в положение M1 и имеет скорость v₁ (рис. 4).