Вектор скорости точки

Рис.4

Рис.3

Рис.1

При движении точки М вектор 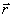будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, 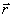является переменным вектором (вектором-функцией), зависящим от аргу­мента :

.

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 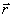и найти положение движущейся точки.

Геометрическое место концов вектора 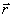, т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

, , .

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор 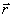на составляющие по осям координат:

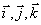где - проекции вектора на оси; – единичные векторы направленные по осям, орты осей.

Так как начало 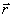вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

Пример 1.Движение точки задано уравнениями

Чтобы исключить время, параметр t, найдём из первого уравнения из второго Затем возведём в квадрат и сложим. Так как 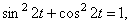получим Это уравнение эллипса с полуосями 2 см и 3 см (рис.2).

Начальное положение точки M₀ (при t=0) определяется координатами

Рис.2Через 1 сек. точка будет в положении M₁ с координатами

 

Примечание.

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.

3. Естественный способ задания движе­ния точки.

 

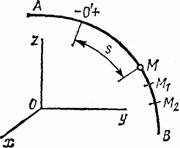
Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О' до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

.

Уравнение выражает закон движения точки М вдоль тра­ектории.

Пример 2. Точка движется по прямой линии, по закону (рис. 4).

 

В начале движения, при 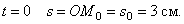Положение точки M₀ назы­вается начальным положением. При

Конечно, за 1 сек. точка прошла расстоя­ние M₀M₁=2 см. Так что s – это не путь пройденный точ­кой, а расстояние от начала отсчёта до точки.

 

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки.

Известно, что при движении точки по прямой линии с постоянной скоростью, равномерно, скорость её определяется делением пройденного расстояния s на время: . При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится