Понятие союзной системы координат
Союзная система координат и ее связь с основной
Введем аффинную систему координат с полюсом в точке  и базисными векторами, совпадающими с
и базисными векторами, совпадающими с  .
.
Эта система координат называется союзной по отношению к исходной, т.е. основной, системе координат с базисом 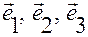 и полюсом в точке
и полюсом в точке  .
.
Матрицу метрических коэффициентов союзной системы будем обозначать  , а элементы этой матрицы —
, а элементы этой матрицы —  ,
,  .
.
Так что будем иметь:
 ,
,  ,
, 
 .
.
Пусть  — координаты вектора
— координаты вектора  в союзной системе координат, и
в союзной системе координат, и  — координаты этого вектора в основной системе координат, другими словами - его контравариантные координаты.
— координаты этого вектора в основной системе координат, другими словами - его контравариантные координаты.
Покажем, что координаты вектора  в союзной системе совпадают с его ковариантными координатами, т.е. справедлива формула
в союзной системе совпадают с его ковариантными координатами, т.е. справедлива формула
 ,
, 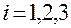 . (1.5.20)
. (1.5.20)
Действительно, по определению координат вектора  в союзной системе можем записать
в союзной системе можем записать
 .
.
Умножая это равенство скалярно на  , слева (по определению ковариантных координат вектора
, слева (по определению ковариантных координат вектора  ) будем иметь
) будем иметь
 ,
,
где 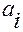 —
—  -я ковариантная координата вектора
-я ковариантная координата вектора  .
.
Учитывая (1.5.17):
 (1.5.17)
(1.5.17)
справа получим
 .
.
Таким образом, равенства (1.5.20) доказаны.
7.3.2. Связь между матрицами  и
и 
Докажем справедливость соотношения
 . (1.5.21)
. (1.5.21)
Действительно, для любого вектора  можем записать
можем записать
 . (1.5.22)
. (1.5.22)
Умножая (1.5.22) последовательно (для  ) скалярно на
) скалярно на  , получим
, получим
 ,
, 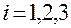 .
.
Эта система в матричном представлении имеет вид:

 . (1.5.23)
. (1.5.23)
Умножая (1.5.22) последовательно (для  ) скалярно на
) скалярно на  , находим
, находим
 ,
,  .
.
Соответственно, в матричном представлении имеем:
 .
.
Подставляя в левую часть соотношение (1.5.23), придем к системе
 ,
,
где  — единичная матрица размерности
— единичная матрица размерности  .
.
В силу произвольности вектора  получаем
получаем
 .
.
Отсюда следует справедливость соотношения (1.5.21)
 . (1.5.21)
. (1.5.21)
Докажем следующее утверждение.
Прежде чем формулировать его, проделаем построения:
· по заданной исходной основной системе координат построим союзную систему;
· построенную союзную систему возьмем в качестве новой основной;
· по ней построим систему, союзную к этой новой основной.