Определение 1
Круговое движение точки
В этом параграфе на примере кругового движения точки будем рассматривать задание ее движения различными способами.
Круговое движение является частным случаем плоского движения точки.
1º . Система отсчета для описания плоского движения точки
Движение материальной точки называется плоским, если траектория этой точки является плоской кривой.
Плоскость, в которой совершает свое движение точка, является соприкасающейся плоскостью ее траектории.



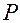
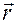






|







 Рис. 1.3.1
Рис. 1.3.1
Для описания плоского движения, как правило, используется следующая система отсчета (см. рис.1.3.1).
За начало отсчета (точка  ) выбирается какая-либо точка в плоскости движения.
) выбирается какая-либо точка в плоскости движения.
В системе отсчета плоского движения:
· плоскость  совпадает с соприкасающейся плоскостью траектории;
совпадает с соприкасающейся плоскостью траектории;
· оси  и
и  взаимно ортогональны и имеют
взаимно ортогональны и имеют  направляющие орты
направляющие орты  и
и  .
.
· Ось  ортогональна плоскости движения, и направляющий орт
ортогональна плоскости движения, и направляющий орт  дополняет систему
дополняет систему  до правой.
до правой.
Орт  оси
оси  определяет в абсолютном пространстве ориентацию плоскости движения точки.
определяет в абсолютном пространстве ориентацию плоскости движения точки.
· Часто в плоскости движения в рассмотрение вводится угол поворота
 радиус-вектора
радиус-вектора 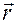 точки
точки 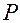 относительно произвольно выбранного, фиксированного вектора
относительно произвольно выбранного, фиксированного вектора  .
.
· В зависимости от ориентации плоскости движения (в зависимости от направления орта  ) задается правило выбора положительного направления изменения угла поворота (см. ниже, определение 3 в п.2º).
) задается правило выбора положительного направления изменения угла поворота (см. ниже, определение 3 в п.2º).