Алгоритм построения радиуса кривизны кривой

 

Алгоритм расчета величины радиуса кривизны 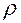в регулярной точке кривой строится на основе кинематических формул (1.2.17) и (1.2.18).

Пусть гладкая кривая задается параметрическим способом:

 

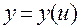, , , . (1.2.19)

 

1). Задаем какое-либо движение 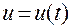по кривой.

Например, в качестве берем функцию .

 

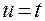2). Вычислим величины и .

 

На заданном движении, будем иметь:

, , .

 

Здесь 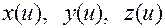— заданные функции (1.2.19).

По величинам , , находим :

Аналогично, для вычисления ускорения дифференцированием координат скорости находим выражения для координат ускорения:

,

, (1.2.20)

.

Подставляя правые части (1.2.20) в формулу для квадрата модуля ускорения:

,

вычисляем .

3). Определяем величину .

Формулу для расчета получаем через последовательность следующих очевидных соотношений:

 

.

4). Значение радиуса кривизны получим подстановкой вычисленных значений величин , , в формулу (1.2.17):

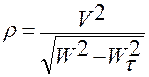. (1.2.17)