Кинематическая формула радиуса кривизны
Естественный способ задания движения точки
5º. Кинематический способ вычисления кривизны кривой
Из формулы Гюйгенса (1.2.16)
 (1.2.16)
(1.2.16)
находим

 . (1.2.17)
. (1.2.17)
Покажем, что

 . (1.2.18)
. (1.2.18)
Действительно, из (1.2.15):
 , (1.2.15)
, (1.2.15)
следует соотношение
 .
.
Дифференцируя это равенство по 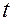 , получим
, получим
 .
.
Возводим в квадрат и, учитывая, что
 ,
,
приходим к соотношению
 .
.
Отсюда следует равенство (1.2.18):
 .
.
Таким образом, формула (1.2.17):

 , (1.2.17)
, (1.2.17)
где

 , (1.2.18)
, (1.2.18)
позволяет вычислить радиус кривизны, если известны  ,
,  и
и  .
.