Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Рис.28

Рис.27

 

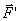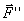Приложим к этой точке две урав­новешивающиеся силы и , парал­лельные силе 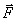и равные ей по вели­чине: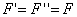

В результате получим силу , приложенную к точке О. То есть мы как бы перенесли заданную силу 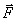из точки А в точку О, но при этом появилась пара, образованная си­лам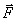и и 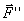. Момент этой пары 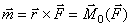, равен моменту заданной силы 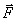относительно точки О.

Этот процесс замены силы 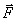равной ей силой 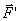и парой называ­ется приведением силы к точке О.

Точка О называется точкой приведения; сила 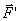, приложенная к точке приведения, – приведённой силой. Появившаяся пара – присоеди­нённой парой.

 

Приведение плоской системы сил к данному центру.

Пусть на твердое тело действует какая-нибудь систем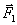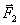а сил , , …, , лежащих в одной плоскости. Возьмем в этой плоскости произвольную точку О, которую назовем центром приведения, и, перенесем все силы в центр О (рис. 28, а). В результате на тело будет действовать система сил 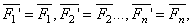приложенных в центре О, и система пар, моменты которых будут равны: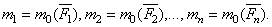

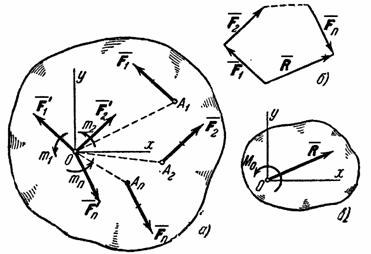
Силы, приложенные в центре О, можно заменить одной силой 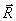,приложенной в том же центре; при этом 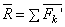или

Точно так же, по теореме о сложении пар, все пары можно заменить одной парой, лежащей в той же плоскости. Момент этой пары 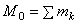или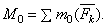

Величина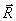, равная геометрической сумме всех сил системы, называется, как известно, главным вектором системы; величину М_о, равную сумме моментов всех сил системы относительно центра О, будем называть главным моментом системы относительно цент­ра О. В результате мы доказали следующую теорему: всякая пло­ская система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М₀, равным главному моменту системы относительно центра О (рис. 28, в).

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.

Здесь О - любая точка плоскости.

Найдем вытекающие из равенств аналитические условия равновесия.

Величины R и М_о определяются равенствами:

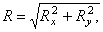
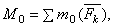
где 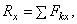Но R может равняться нулю только тогда, когда одновременно R_x = 0 и R_y = 0. Следовательно, условия будут выполнены, если будет:

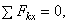
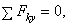
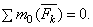
Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

; ;
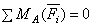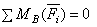