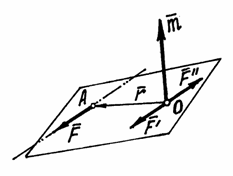
Теорема о параллельном переносе силы.

Рис.26

Рис.25

 

Рис. 4.4.

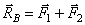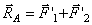Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие и . Так как , то эти силы 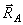и 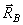будут образовывать пару, мо­мент которой 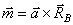, где 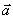– радиус-вектор точки В, совпадающий с АВ.

Так как 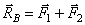, то момент полученной пары

.

Следовательно, в результате сложения пар, расположенных в пере­секающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоско­стях, получим пару с моментом

.

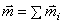Конечно, эта результирующая пара будет располагаться в плоско­сти перпендикулярной вектору .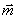

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие рав­новесия пар

.

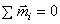Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.

 

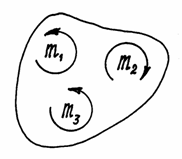
Например, пары, показанные на рис.26, расположены в одной плоскости и моменты их:

m₁=2 Hсм , m₂=5 Hсм, m₃=3 Hсм. Пары урав­нове­шива­ются, потому что алгебраиче­ская сумма их моментов равна нулю:

.

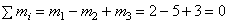Равнодействующая системы сходящихся сил непосредственно находится с помощью аксиомы параллелограмма сил. Для двух параллельных сил эта задача была решена путем приведения их к сходящимся силам. Очевидно, что анало­гичную задачу легко будет решить и для произвольной системы сил, если найти и для них метод приведения к силам, приложенным в одной точке.

Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.

Попробуем силу 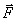(рис. 27) перенести в какую-нибудь точку О, не расположенную на линии дей­ствия.