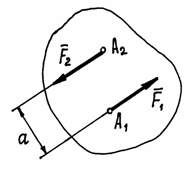
Пара сил. Момент пары.

Рис.21

 

Рассмотрим систему сил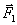, , 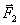…, , сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие выражения моментов m₀(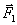), m₀(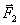), … . По формуле . Но, как видно из рисунка, 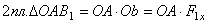, где F_1x - проекция силы 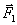на ось Ох; сле­довательно

.

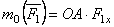Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил 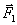, , 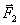…, , через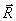, где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

или,

.

 

Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис.22). Очевидно, , 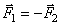и 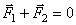.