Термодинамические потенциалы.

Энтропия. Общая формулировка второго закона (начала) термодинамики.

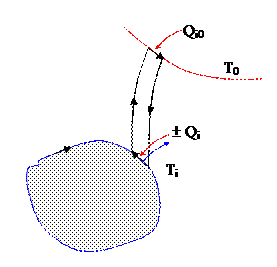Можно показать, что для замкнутого равновесного цикла справедливо следующее интегральное соотношение

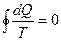(2)
(dQ – дифференциальная теплота обмена с источником при температуре T). Доказательство проводится по схеме, представленной на рисунке. Основной цикл совмещают с дифференциальными циклами Карно между базовой температурой T₀ и температурой T_i участка цикла. При этом теплоты принятые и отданные на участке основного цикла делают равными. Известно, что для цикла Карно

.

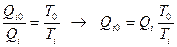В результате такого «сложного» цикла система получает тепло 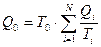и полностью превращает его в работу, что запрещено постулатом Клаузиуса (вторым началом термодинамики). Поэтому должно выполняться условие (2), определенное выше. Формула (2) позволяет ввести в термодинамику понятие энтропии, как функции состояния системы.

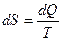(3)
При дифференциальном (равновесном) обмене теплотой с источником изменение энтропии системы равно . Для двух произвольных состояний системы изменение энтропии в ходе равновесного перехода записывается интегралом

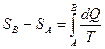. (4)
Если процесс перехода в новое состояние не является равновесным, то соотношение (4) должно записываться в виде неравенства

. (5)
Для теплоизолированной системы получаем

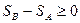. (6)
Изменение энтропии замкнутой системы возможно только при условии, что система находилась в неравновесном состоянии. Потому, энтропия изолированной неравновесной системы при переходе к равновесию увеличивается.

Соотношение (6) является наиболее общей формой второго начала термодинамики и называется неравенством Клаузиуса.

Использование формулы (3) позволяет записывать первый закон термодинамики для равновесных процессов с использованием дифференциала энтропии (для газа)[10]

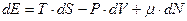. (7)

 

6.Третье начало термодинамики. (сформулировано В.Г. Нернстом в 1906 году) При приближении температуры к 0 К энтропия стремится к определенному пределу. Равновесные процессы при 0 К проходят без изменения энтропии. Энтропия при 0 К не зависит от значений параметров, характеризующих состояние системы (объема, давления и т.д.). Числовое значение энтропии при 0 К не фиксировано, но его удобно выбрать равным нулю.[11]

 

 

В термодинамике чаще всего используют четыре энергетические функции, называемые термодинамическими потенциалами: энергия, свободная энергия Гельмгольца, термодинамический потенциал Гиббса (большой потенциал), энтальпия (тепловая функция).

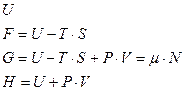. (8)
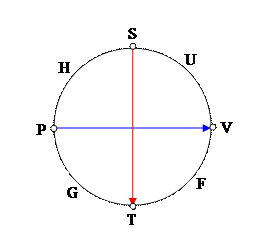
Дифференциалы этих потенциалов можно получить, используя мнемоническую схему Максвелла.

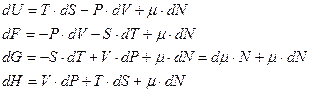. (9)
Символ термодинамического потенциала стоит между двумя величинами, которые «образуют» дифференциалы. Множители дифференциалов стоят напротив величин. Знак слагаемого определяется направлением стрелок. «Движение» от дифференциала к множителю против стрелки дает знак минус (по стрелке плюс). Треть слагаемое у всех дифференциалов одинаковое. Формулы (9) уточняют определение химического потенциала. Наиболее «понятное» определение получается на основе термодинамического потенциала Гиббса.

m - численно равно удельному изменению потенциала Гиббса при условиях постоянства температуры и давления.

Смысл введения термодинамических потенциалов состоит в следующем. При различных условиях равновесие системы соответствует минимуму некоторого термодинамического потенциала.