Лекция 5
Рис. 1.23. К определению момента силы относительно точки
По определению векторного произведения вектор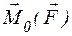 
приложен в точке O и направлен перпендикулярно плоскости, содержащей перемножаемые векторы ( плоскость треугольника OАВ) в ту сторону, откуда поворот от вектора 
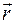к вектору 
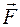виден происходящим против хода часовой стрелки (рис.1.23). Модуль вектора-момента равен:
,
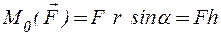где h - плечо силы 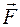относительно точки O.
Введенный таким образом момент, полностью определяет вращательный эффект приложенной к телу силы: его линия действия определяет плоскость вращения, его направление - направление вращения, его модуль - интенсивность вращательного воздействия силы на тело.
3. Теорема Вариньона для системы сходящихся сил
Момент равнодействующей, относительно некоторой точки О, равен сумме моментов составляющих сил относительно той же точки.
Данная теорема справедлива для любой системы сил, имеющей равнодействующую. Приведем здесь ее доказательство для системы сходящихся сил.
Пусть 
является равнодействующей системы сходящихся сил 
, т.е.
.
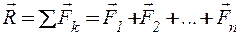Тогда по определению момента
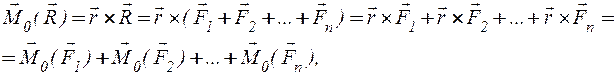
что и требовалось доказать.
4. Момент силы относительно оси
Моментом силы относительно оси называется проекция на эту ось вектора момента данной силы относительно любой точки, лежащей на этой оси.
Пусть необходимо вычислить момент силы относительно оси Z. Выберем на этой оси (рис. 1.24) произвольную точку O и проведем через нее оси X и Y. По определению момент силы относительно точки O равен векторному произведению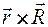 
:
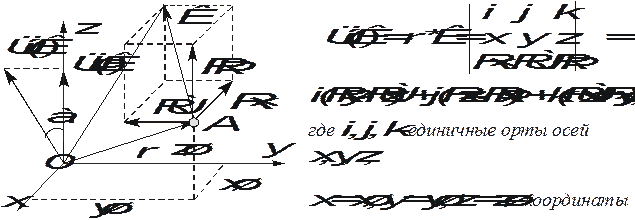
Рис. 1.24. Определение осевых моментов
Из векторной алгебры известно, что выражения, стоящие в скобках при единичных ортах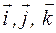 
представляют собой проекции векторного произведения на оси x, y, z соответственно:
,
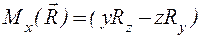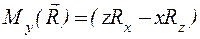, (1.3)
.
Анализируя последнее из выражений (1.3) можно заметить, что оно не содержит координаты z. Это значит, что значение осевого момента Mz не зависит от выбора точки О на оси z. Отсутствие в данном выражении Rz говорит о том, что осевой момент создают лишь перпендикулярные данной оси составляющие силы. Это означает, что если сила параллельна какой-либо оси, то ее момент относительно этой оси равен нулю. Кроме того, отсюда же (и из теоремы Вариньона) следует простое правило вычисления осевых моментов:
Момент силы ™ относительно какой-либо оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси, взятому относительно точки пересечения оси с плоскостью.
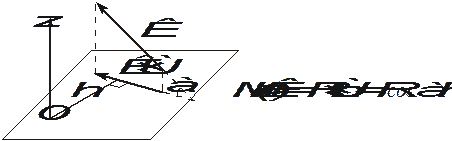
Рис. 1.25. Вычисление осевого момента
Момент будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила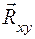 
, виден происходящим против хода часовой стрелки. Из рис. 1.25 видно, что если линия действия силы 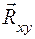, а, следовательно и силы , пересекает ось Z, то ее осевой момент будет равен нулю ( т.к. в этом случае h = 0 ).