Реакции геометрических связей

Сила, с которой данная связь действует на тело, препятствуя его перемещению, называется силой реакции связи или просто реакцией связи. Значения реакций связей определяются в процессе решения соответствующей задачи механики. Направлена же реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Ниже представлены наиболее часто встречающиеся типы связей и направления их реакций.

 

Рис. 1.12

 

Гладкая плоскость (поверхность или опора) (рис. 1.12). Реакция 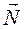гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке.

 

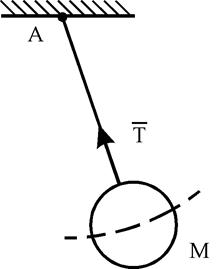Рис. 1.13

Нить (канат, цепь, ремень, трос). Связь, осуществленная в виде гибкой нерастяжимой нити (рис. 1.13), не дает телу М удаляться от точки подвеса нити по направлению АМ. Поэтому реакция 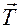натянутой нити направлена вдоль нее от тела к точке подвеса.

Неподвижный цилиндрический шарнир или подшипник (шарнирно-неподвижная опора). Цилиндрическим шарниром (рис. 1.14) называется совокупность неподвижной обоймы (втулки) 1 и помещенного в нее валика (пальца) 2, жестко соединенного с телом 3. В точке С соприкосновения втулки с валиком возникает сила опорной реакции, направленная по нормали к идеально гладким поверхностям. Эта нормаль проходит через геометрический центр А валика. Так как положение точки С соприкосновения валика со втулкой заранее не известно, то невозможно сразу указать направление силы реакции 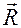, но можно утверждать, что линия действия реакции 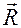всегда пройдет через центр А шарнира. На расчетных схемах шарнирно-неподвижная опора условно изображается так, как показано на рис. 1.15. Неизвестную по модулю и направлению реакцию 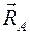при решении задач представляют в виде двух ее взаимноперпендикулярных составляющих 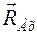и . 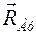После определения их значений находят значение реакции 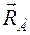и ее направление:

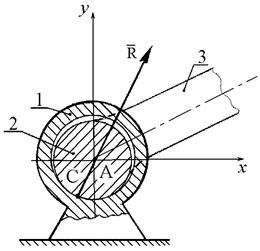Рис. 1.14 Рис. 1.15

 

,

 

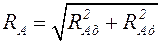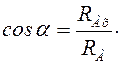
Шарнирно-подвижная опора (опора на катках). Реакция 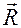такой связи проходит через центр шарнира (рис.1.16) и направлена перпендикулярно к опорной

Рис. 1.16

 

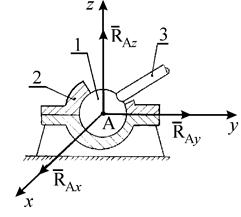Рис. 1.17

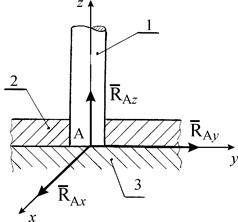Рис. 1.18

Сферический шарнир (рис. 1.17). Сферическим шарниром называется устройство, выполненное в виде двух контактирующих сфер, геометрический центр А которых неподвижен. Тело 3, равновесие которого рассматривается, жестко связано с внутренней подвижной сферой 1. При условии, что сферические поверхности гладкие, реакция 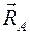направлена по нормали к этим поверхностям и проходит через центр А сферы. На расчетных схемах реакцию 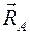представляют в виде трех ее взаимно-перпендикулярных составляющих 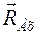, 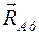и 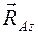, направленных вдоль координатных осей.

Подпятник (рис. 1.18). Подпятник представляет собой соединение цилиндрического шарнира 2 и опорной плоскости 3, на которую опирается вал 1. Реакция подшипника, лежащая в плоскости перпендикулярной оси вала, представляется двумя ее взаимно-перпендикулярными составляющими и 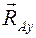, а реакция опорной плоскости - реакцией 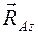, направленной по нормали к этой плоскости.

Невесомый стержень (рис. 1.19). Реакция 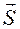прямолинейного невесомого (идеального) стержня направлена вдоль этого стержня. Если связью является криволинейный стержень, то реакция направлена вдоль прямой АВ, соединяющей концевые шарниры А и В.

 

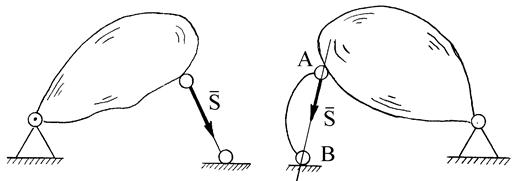
Рис. 1.19

Жесткая заделка (неподвижное защемление) конца балки (рис. 1.20). Такая связь не допускает не только линейных перемещений балки 1 вдоль координатных осей, но и вращения балки в плоскости хАу.

 

 

Рис. 1.20

 

Нахождение реакций жесткой заделки сводится к определению трех неизвестных величин: составляющих и реакции 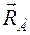и так называемого реактивного момента М_А, препятствующего вращению балки в плоскости хАу вокруг точки А.

 

5.Порядок решения задач статики

Большинство задач статики решаются в следующем порядке:

а). Для решения задачи нужно рассмотреть равновесие твердого тела, к кото-

рому приложены заданные и искомые силы (или силы равные искомым).

б). На чертеже изображаем все силы, приложенные к данному телу, включая

реакции связей.

в). Выбираем систему координат и составляем уравнения равновесия.

г) Решая данную систему уравнений равновесия, определяем искомые величины.

 

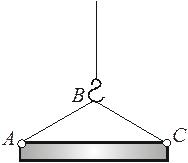
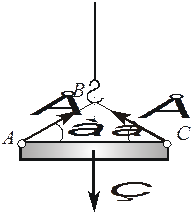
Пример. Однородная балка АС длиной L = 3 м и весом P= 40 кН поднимается вверх с помощью крана. Определить минимальную длину троса АВС, при котором возможен подъем балки, если трос выдерживает натяжение T = 30 кН.

Решение. Рассмотрим равновесие балки, поскольку именно к ней приложены заданная сила (вес балки) и силы натяжения троса. Пусть оси системы координат направлены как обычно: ось x вправо, ось y - вверх. Тогда уравнения равновесия запишутся в виде:

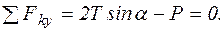
Подставляя во второе уравнение численные значения веса Р и максимальное значение силы натяжения Т, определяем значение sina, а затем и минимальную длину троса: