Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Геометрические условия равновесия.

Для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая (а, следовательно и главный вектор данной системы сил) были равны нулю.

Условия, которым при этом должны удовлетворять силы системы, можно выразить в геометрической и в аналитической форме.

 

 

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из сил системы, был замкнутым. Это означает равенство нулю равнодействующей и главного вектора данной системы сил. Напомним, что векторная сумма - это вектор, соединяющий конец последнего из слагаемых векторов с началом первого из них.

 

Аналитические условия равновесия.

Очевидно [см. формулы (1.1)], что равнодействующая системы сходящихся сил и ее главный вектор будут равны нулю, если суммы проекций всех сил на координатные оси будут равны нулю, т.е.

å F_kx = 0 , å F_ky = 0, å F_kz = 0 . (1.2)

Равенства (1.2) выражают условия равновесия системы сходящихся сил в аналитической форме.

 

3.Теорема о трех силах

Доказательство.

Так как по условию теоремы все три силы непараллельны, перенесем две любые из них в точку пересечения их линий действий (на рис 1.11 силы А! и А@ переносятся в точку Е) и заменим равнодействующей ™. Поскольку тело по условию находится в равновесии, а операция по переносу сил вдоль линий их действия и последующего сложения этого равновесия не нарушит, то линия действия третьей силы А# должна пройти через точку Е в соответствие с первой аксиомой статики.

 

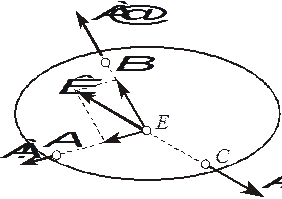
Рис. 1.11. К доказательству теоремы о трех силах