СТАТИКА

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Лектор: старший преподаватель Какурина Светлана Константиновна

КУРС ЛЕКЦИЙ

По дисциплине: «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»

Раздел: «СТАТИКА»

Для студентов всех специальностей

дневного и заочного обучения

Красноярск 2012г.

1. Яблонский А.А., Никифорова В.М. Я 14 Курс теоретической механики. Учебник для техн. вузов. – 7-е изд. стереотипное. – Серия «Учебники для вузов. Специальная литература». – СПб.: Издательство «Лань», 1999. – 768 с.

2. Тарг С.М. Курс теоретической механики. М., 1963 и последующие издания.

3. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах, ч. I и II. М., 1961 и последующие издания.

4. Сборник заданий для курсовых работ по теоретической механике / Под ред. проф. А.А. Яблонского. М., 1968 и последующие издания.

Статикой называется раздел теоретической механики, в котором изучаются условия равновесия систем сил, приложенных к твёрдым телам.

1. Основные понятия статики.

1. Материальное тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.

2. Материальное тело, расстояние между двумя любыми точками которого не изменяется при любых механических воздействиях, называется абсолютно твёрдым телом.

3. Сила – мера механического взаимодействия тел. Характеризует интенсивность и направление этого взаимодействия. Величина векторная. Различают три основных элемента силы:

- модуль, т.е. численное значение;

- направление;

- точку приложения.

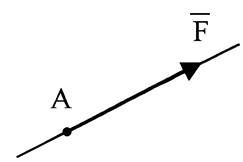
Линия, вдоль которой направлена сила –

линия действия силы.

Единицы измерения силы – Н, кН.

4. Совокупность сил, действующих на тело, называется системой сил.

5. Если, не изменяя состояния тела одну систему сил можно заменить другой системой, то эти системы называются эквивалентными. (Состояние – кинематическое состояние некоторого движения или покоя).

6. Если под действием данной системы сил тело находится в равновесии, то эту систему называют уравновешенной или эквивалентной нулю.

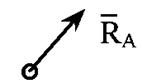
7. Сила, равная данной системе сил, называется равнодействующей – R.

2. Аксиомы статики.

1. Для равновесия тела под действием двух сил необходимо и достаточно, чтобы эти силы были равны по модулю и противоположно направлены по прямой, соединяющей их точки приложения.

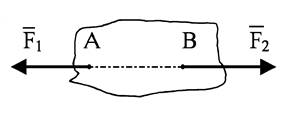
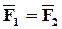
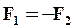
Это уравновешивающиеся силы.

2. Не нарушая состояния тела, можно добавлять или отбрасывать уравновешивающиеся силы.

Следствие: не нарушая состояния тела, силу можно переносить по её линии действия в любую точку тела.

3. Равнодействующая двух сил, приложенных к телу в одной точке, приложена к той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой диагонали.

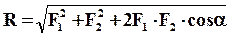
4. Два тела действуют друг на друга с силами равными по величине и направленными по одной прямой в противоположные стороны.

5. Равновесие нетвёрдого тела не нарушится при его затвердевании.

3. Связи и реакции связей.

Твёрдое тело называется свободным, если его движение ничем не ограничено. При решении многих технических задач встречаются несвободные твёрдые тела. Несвободным называется такое тело, на которое наложены связи, ограничивающие его движение в некоторых направлениях. Тело, ограничивающее движение данного тела, называется связью. Сила, с которой связь действует на тело, называется реакцией связи.

Принцип освобождаемости от связей. Всякое несвободное тело, можно считать свободным, если отбросить связи и заменить их действие на тело реакциями связи.

Примеры связей и их реакций.

1) гладкая поверхность:

2) точечная опора:

3) гибкая связь:

4) стержневая связь:

5) цилиндрическая шарнирно-подвижная опора:

6) цилиндрическая шарнирно-неподвижная опора и подпятник:

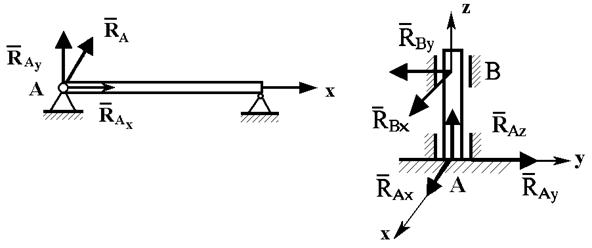
7) сферический шарнир:

8) жёсткая или глухая заделка:

9) прочие:

4. Система сходящихся сил.

Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

4.1. Геометрический способ определения равнодействующей

системы сходящихся сил.

Найти равнодействующую – значит сложить силы.

1) сложение двух сил:

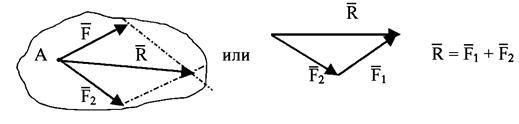
2) сложение трёх сил, не лежащих в одной плоскости:

3) сложение системы сходящихся сил:

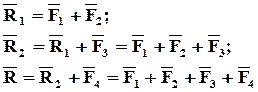
Вывод: равнодействующая нескольких сходящихся сил по величине и направлению выражается вектором, соединяющим начальную и конечную точки ломаной линии, сторонами которой служат векторы, соответствующие данным силам. Это правило силового многоугольника.

4.2. Условие равновесия системы сходящихся сил

в геометрической форме.

Для того, чтобы с.с.с. находилась в равновесии необходимо и достаточно, чтобы R = 0, т.е., чтобы многоугольник был замкнутым.

4.3. Проекция силы на ось и на плоскость.

Сила и ось Х лежат в одной плоскости. Спроецируем силу на ось. Проекцией силы на ось называется взятая со знаком + или -величина отрезка, заключённого между проекциями начала и конца этой силы на ось. Если направление вектора силы совпадает с

направлением оси, то проекция +. Проекция силы на ось величина скалярная.

F_x= ав = F ^.cos a.

Спроецируем силу 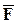на плоскость XOY. Проекцией силы на плоскость называется вектор, заключённый между проекциями начала и конца этой силы на плоскость. Модуль проекции равен произведению модуля проецируемой силы на сos острого угла между направлением силы и направлением проекции.

Для того, чтобы спроецировать силу на ось Х, можно воспользоваться методом двойного проецирования.

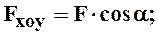
4.4. Аналитический способ задания сил.

Для аналитического способа задания сил необходимо:

1) выбрать систему координатных осей;

2) задать модуль силы F и углы, которые сила образует с координатными осями (α, β, γ);

3) задать координаты точки приложения силы.

При решении задач удобнее задавать силу её проекциями на координатные оси F_x ; F_y ; F_z . Зная проекции, легко определить модуль силы и углы, которые она образует с координатными осями.

Если сила лежит в плоскости, то:

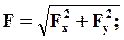
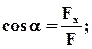
4.5. Аналитический способ сложения сил.

Теорема: Проекция равнодействующей на какую-либо ось равна алгебраической сумме проекций составляющих сил на ту же самую ось. Согласно этой теореме:

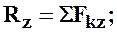
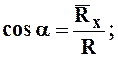
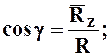
4.6. Условие равновесия системы сходящихся сил в аналитической форме.

Как известно, для того, чтобы с.с.с. находилась в равновесии необходимо, чтобы равнодействующая этой системы была равна нулю.

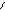
Отсюда:

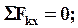
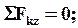
Для того, чтобы пространственная с.с.с. находилась в равновесии необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из координатных осей была равна нулю.

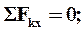
- пл. с.с.с.

5. Момент силы.

5.1. Алгебраический момент силы относительно точки.

Алгебраическим моментом силы относительно точки называется взятое со знаком + или - произведение модуля этой силы на её плечо.

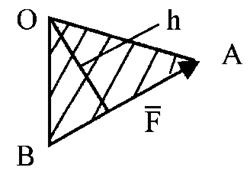Плечом силы называется длина перпендикуляра опущенного из этой точки на линию действия силы. Момент считается +, если сила стремится повернуть плоскость, проходящую через точку и линию действия силы, против хода часовой стрелки и - , если по ходу.

Свойства момента силы:

1. Численное значение момента силы относительно точки равно удвоенной площади треугольника, полученного соединением данной точки с началом и концом вектора силы.

2. Момент силы относительно точки равен нулю, если линия действия проходит через эту точку.

3. Момент силы относительно точки не изменится, если силу перенести вдоль линии её действия.

5.2. Векторный момент силы относительно точки.

Векторным моментом силы относительно точки

называется вектор, приложенный в этой точке и

равный по модулю произведению модуля силы на

её плечо, направленный по перпендикуляру к плос-

кости, проходящей через данную силу и точку, в ту

сторону, чтобы глядя навстречу этому вектору ви-

деть силу, вращающей эту плоскость вокруг данной точки против хода часовой стрелки.

5.3. Момент силы относительно оси.

Пусть на тело, имеющее ось вращения Z в точке А действует сила F. Проведём через точку А плоскость перпендикулярную оси Z. Точка пересечения плоскости с осью – точка О. Разложим силу на её составляющие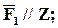

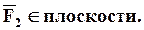
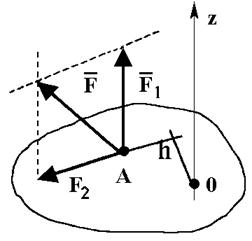Сила не создаёт вращения вокруг оси Z, она стремится сдвинуть тело вдоль оси. Вращательный эффект создаёт сила 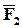относительно этой оси. Моментом силы относительно оси называется момент проекции этой силы на плоскость перпен-дикулярную оси относительно точки пересечения этой оси с плоскостью. Момент берётся со знаком +, если глядя с положи- тельного конца оси мы видим силу вращаю- щей плоскость против хода часовой стрелки и со знаком -, если по ходу часовой стрелки.

Момент силы относительно оси равен нулю, если:

1) проекция силы равна нулю, т.е. сила параллельна оси;

2) плечо равно нулю, т.е. проекция силы пересекает ось.

6. Система параллельных сил.

Система сил, линии действия которых параллельны, называется системой параллельных сил.

6.1. Сложение двух параллельных сил.

1) направленных в одну сторону:

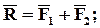
2) направленных в противоположные стороны (антипараллельных):

7. Пара сил.

Две равные по модулю антипараллельные силы называются парой сил.

Свойства пары сил:

- пару сил нельзя заменить одной равнодействующей силой;

- пара сил создаёт вращательный эффект;

- плоскость, в которой лежит пара сил, называется плоскостью действия пары;

- эффект действия пары сил на тело определяется моментом.

Моментом пары сил называют взятое со знаком + или - произведение модуля одной из сил пары на её плечо. Плечом называют кратчайшее расстояние между линиями действия пары.

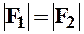
Момент берётся со знаком + , если пара пытается повернуть плоскость действия против хода часовой стрелки и со знаком - , если по ходу часовой стрелки.

Теория пар сил на плоскости сводится к четырём теоремам:

Теорема 1. Алгебраическая сумма моментов сил, составляющих пару, относительно произвольной точки плоскости не зависит от выбора этой точки и равна моменту пары сил.

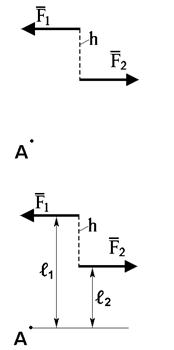На плоскости действуют пара сил F₁ = F₂. На этой же плоскости возьмём произвольную точку А.

Обозначим расстояния от точки А до сил F₁иF₂черезℓ₁иℓ₂.

Запишемуравнение моментов относительно точки А.

1)

выразим ℓ₁черезℓ₂

ℓ₁ = ℓ₂ + h , подставим в (1), учитывая, что .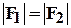

Теорема 2. Не нарушая состояния твёрдого тела, пару сил можно переносить в плоскости её действия.

Теорема 3. Пары сил, моменты которых равны, эквивалентны.

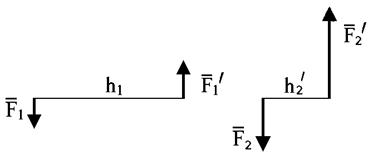
Это значит, что, не нарушая состояния тела, можно изменить величину плеча либо величину силы, сохраняя при этом момент пары сил.

Теорема 4. При сложении нескольких пар сил на плоскости получается равнодействующая пара, момент которой равен сумме моментов слагаемых пар.

8. Приведение системы сил к центру.

8.1. Теорема о параллельном переносе сил.

Действие силы на твёрдое тело не изменится, если её перенести параллельно самой себе в любую другую точку этого тела, приложив при этом пару сил, момент которой равен моменту заданной силы относительно центра приведения.

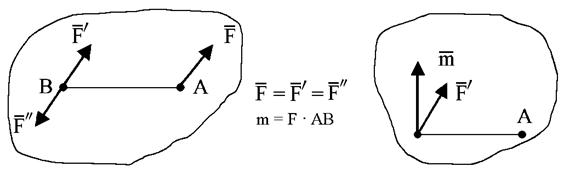
Пусть на тело в точке А действует сила 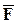. Приложим в точке В равную ей по величине и направлению силу 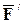. Чтобы действие силы на тело не изменилось, уравновесим силу равной по величине, но направленной противоположно силой . Силы и составляют пару сил с моментом m = F ^. АВ.

8.2. Приведение системы сил к центру.

Пусть на твёрдое тело действует произвольная система сил.

Выберем точку О за центр приведения, и используя теорему о параллельном переносе сил, перенесём все силы в центр О. Тогда на тело будет действовать

система сил, приложенных в цент-

ре О, и система пар сил.

Сходящиеся силы, приложенные в точке О заменяются одной силой приложенной в точке О.

Система пар заменится одной парой

Величина R , равная геометрической сумме всех сил, называется главным вектором системы сил. Величина М₀ , равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно центра О.

Таким образом, любая система сил, действующих на абсолютно твёрдое тело, заменяется одной силой, равной главному вектору системы сил, приложенной в центре приведения и одной парой с моментом равным главному моменту системы сил относительно центра.

Сила R не является здесь равнодействующей данной системы, т.к. заменяет систему сил не одна, а вместе с парой сил.

Если для заданной системы сил R = 0, M₀ ¹ 0, то она приводится к одной паре сил с моментом М₀ . Если для заданной системы сил R ¹ 0, а М₀=0, то она приводится к одной силе, т.е. к равнодействующей = R .

9. Условие равновесия системы сил.

Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и её главный момент относительно любого центра были равны нулю, то есть:

R = 0; М₀ = 0.

Условия являются необходимыми, так как если какое-нибудь из них не выполняется, то система сил приводится либо к равнодействующей (когда R¹0), либо к паре сил с моментом М₀ (когда М₀¹0), и следовательно не является уравновешенной. Одновременно условия являются и достаточными, потому что при R = 0 система сил может приводиться только к паре сил с моментом М₀ а так как М₀ = 0, то имеет место равновесие.

9.1. Теорема о моменте равнодействующей (теорема Вариньона).

Момент равнодействующей системы сил относительно центра равен сумме моментов сил системы относительно того же центра.

Система сил приводится к

равнодействующей в точке С. Приложим уравновешивающую силу . Тогда система сил будет находиться в равновесии и для неё должно выполняться условие:

Но т.к. , то следовательно:

9.2. Условие равновесия плоской системы произвольных сил.