Связь тангенциального и углового ускорения.
При вращении за время 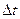 угловая скорость получит приращение
угловая скорость получит приращение 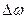 , тогда (8) примет вид:
, тогда (8) примет вид:
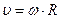

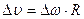 (14)
(14)
Разделим обе части на 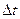 , получим:
, получим:
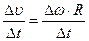 (15)
(15)
или
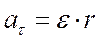 (16)
(16)
Векторное произведение:
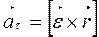 (17)
(17)
Вектор тангенциального ускорения совпадает по направлению с векторным произведением 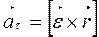 . Векторное произведение всегда связано с правилом правого винта: вращая головку винта по направлению вектора
. Векторное произведение всегда связано с правилом правого винта: вращая головку винта по направлению вектора 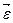 , стоящего на первом месте в (13), к вектору
, стоящего на первом месте в (13), к вектору  , стоящему на втором месте, определяем по поступательному движению винта направление третьего вектора
, стоящему на втором месте, определяем по поступательному движению винта направление третьего вектора 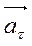 .
.