Определение скоростей и ускорений точки в сложном движении.

Сложное движение точки.

 

1. Во многих задачах механики удобно считать, что движение точки относительно основной (условно неподвижной) системы отсчета состоит из нескольких более простых движений. Для этого вводят в рассмотрение вторую (подвижную) систему отсчета, движущуюся относительно основной. Теперь движение точки относительно неподвижной системы можно рассматривать как сумму одновременно происходящих двух движений: движения относительно подвижной системы отсчета и движения точки вместе с подвижной системой относительно неподвижной. Так, например, можно считать, что движение человека, идущего по эскалатору метро, по отношению к неподвижной стене туннеля (относительно неподвижной системы отсчета) состоит из двух движений, а именно из движения человека относительно движущегося эскалатора (относительно подвижной системы координат) и его движения вместе с эскалатором относительно неподвижной стены. Аналогичным образом могут быть представлены движения человека, плывущего по реке, по отношению к неподвижному берегу, движение поднимаемого мостовым краном груза при одновременном перемещении кран балки, движение снаряда в канале ствола зенитного орудия при одновременном вращении ствола в процессе слежения за целью и т.п.

Такое движение точки, рассматриваемое одновременно в неподвижной и в подвижной системах отсчета, называется сложным или составным. При этом движение точки относительно основной (неподвижной) системы отсчета называется абсолютным. Скорость и ускорение точки в этом движении называется абсолютной скоростью и абсолютным ускорением и обозначаются и соответственно. Движение точки относительно подвижной системы отсчета называется относительным, а скорость и ускорение в этом движении - относительной скоростью и относительным ускорением .

Движение подвижной системы отсчета относительно неподвижной называется переносным движением. Скорость и ускорение той, неизменно связанной с подвижной системой отсчета точки пространства, с которой в данный момент времени совпадает движущаяся точка, называется переносной скоростью и переносным ускорением . Так, в случае движения человека, идущего по эскалатору, переносной скоростью человека будет скорость ступеньки, на которой он в данный момент находится.

2. Пусть в некоторый момент времени t точка М занимает положение, указанное на рисунке 2.32. Ее относительная траектория - кривая АВ , неизменно связанная с подвижной системой координат (на рисунке не показана).

Рис. 2.32. К выводу формул сложения скоростей и ускорений

Найдем абсолютное перемещение точки М за малый промежуток времени Dt = t₁ - t . Точка М, двигаясь по кривой АВ (относительное движение), совершает за промежуток времени Dt относительное перемещение ММ" . В это же самое время сама кривая АВ перемещаясь с подвижными осями (переносное движение) займет положение А₂В₂. В результате этих двух перемещений точка Мзаймет положение М₁, относительно основной неподвижной системы отсчета 0xyz, совершив за время Dt абсолютное перемещение ММ₁. Переносное движение относительной траектории, в свою очередь, можно считать состоящей из поступательной части (перемещение АВ в положение А₁В₁) и вращательной части (перемещение А₁В₁ в положение А₂В₂ вращением вокруг точки М' с мгновенной угловой скоростью ). Из рисунка видно, что если бы кривая АВ двигалась только поступательно, то она за время Dt пришла бы в положение А₁В₁, а точка М - в положение М". Появление перемещения М"M₁, следовательно, обусловлено вращательной частью переносного движения кривой АВ. Из рисунка видно, что абсолютное перемещение точки М за время Dt можно выразить следующим векторным равенством:

 

. (2.45)

 

Известно, что перемещение точки, разлагая его в ряд по степеням малой величины Dt, можно представить в виде

. (2.46)

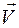где и 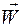- скорость и ускорение точки в момент времени t .

На основании (2.46) абсолютное, относительное и переносное перемещение в (2.45) можно представить в виде :

(2.47)

(2.48)

(2.49)

где ,, , , , - абсолютные, относительные и переносные скорости и ускорения точки М.

Вектор представляет собой перемещение конца радиуса-вектора M'M" при его вращении вместе с кривой A₁B₁ вокруг точки М'. Скорость точки M" в этом вращении определяется формулой Эйлера:

 

. (2.50)

 

Принимая во внимание равенства (2.48) и (2.50) вектор M"M₁ можно представить в виде:

(2.51)

 

С учетом равенств (2.47) - (2.49) и (2.51) выражение (2.45) можно переписать в виде:

 

Приравнивая коэффициенты при одинаковых степенях Dt в левой и правой частях последнего равенства, находим:

 

, (2.52)

 

, (2.53)

 

где вектор называется ускорением Кориолиса. (2.54)

 

Формулу (2.52) называют формулой сложения скоростей точки в сложном движении. Согласно этой формуле, абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей. Формулу (2.53) называют формулой сложения ускорений. Согласно (2.53), абсолютное ускорение точки в сложном движении равно геометрической сумме трех ускорений: относительного, переносного и ускорения Кориолиса. Модуль ускорения Кориолиса согласно (2.54) равен:

 

. (2.55)

 

Очевидно, что данное ускорение равно нулю:

- в случае поступательного переносного движения ( w_e = 0 );

- когда векторы и параллельны ( тогда );

- в отдельные моменты времени, когда относительная скорость меняет свое направление на противоположное и точка (в относительном движении) должна на мгновение остановиться . Направление ускорения Кориолиса определяется по правилу определения направления векторного произведения. Согласно (2.54) вектор направлен перпендикулярно плоскости, в которой лежат перемножаемые векторы и , в ту сторону, откуда поворот от вектора к вектору на наименьший угол виден происходящим против хода часовой стрелки.

. Поскольку в переносном движении точка М вращается по окружности радиуса ОМ с постоянной угловой скоростью Я, переносное ускорение равно и направлено к центру вращения. Модуль ускорения Кориолиса равен 4 м/с², а его направление, определяемое векторным произведением (2.54), показано на рисунке. Так как переносное и кориолисово ускорения направлены под углом 90° по отношению друг к другу, 4,47 м/с².

Пример 2. Кольцо радиуса r = 0,5м вращается с постоянной угловой скоростью Я = 4 рад/с в плоскости чертежа. По кольцу движется точка М с постоянной скоростью V = 2м/с. Определить величину абсолютного ускорения точки М в указанном на чертеже положении.

Решение. В данной задаче движение точки М по кольцу - относительное, вращение вместе с кольцом - переносное. Для определения абсолютного ускорения воспользуемся формулой сложения ускорений:

.

Для изучения относительного движения отвлечемся от переносного т.е. пусть кольцо не вращается, а точка М движется по кольцу с постоянной скорость V=2 м/с. Найденное в этом движении ускорение и будет относительным: . Данное ускорение будет направлено к центру кольца, так как точка в относительном движении движется равномерно. Для определения переносного ускорения отвлечемся от относительного движения точки: точка зафиксирована в положении, указанном на рисунке и лишь вращается вместе с кольцом с постоянной угловой скоростью по окружности радиусом ОМ=2R вокруг точки 0. Найденное в этом движении ускорение и будет переносным: 16м/с². Его направление показано на рисунке и обусловлено равномерной скоростью вращения. Модуль ускорения Кориолиса вычисляем по формуле (2.55):

=(учитываем, что вектор направлен вдоль оси вращения кольца и перпендикулярен вектору ). Направление вектора ,определяемого правилом векторного умножения (2.54), показано на рисунке. Складывая найденные ускорения, определяем